Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

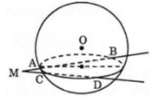
Hai đường thẳng MAB và MCD giao nhau xác định một mặt phẳng (P). Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C), ngoại tiếp tứ giác phẳng ABCD.
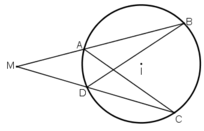
Xét ΔMAC và ΔMDB có:

⇒ MA.MB = MC.MD (đpcm).


Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)

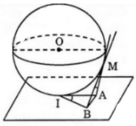
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB ( c.c.c)
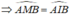

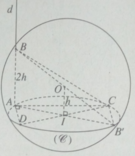
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)






a) Gọi (P) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng (P) cắt mặt cầu S(O;r) theo một đường tròn tâm I, là hình chiếu vuông góc của O lên mặt phẳng (P).
Xét hai tam giác MAD và MCB có góc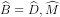 chung nên hai tam giác đó đồng dạng.
chung nên hai tam giác đó đồng dạng.
Vì vậy: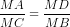 => MA.MB = MC.MD.
=> MA.MB = MC.MD.
b) Đặt MO = d, ta có Oi vuông góc với (P) và ta có:
MO2= MI2 = OI2 và OA2 = OI2 + IA2
Hạ IH vuông góc AB, ta có H là trung điểm của AB.
Ta có MA = MH - HA; MB = MH + HB = MH + HA.
Nên MA.MB =
MH2 – HA2 = (MH2 + HI2) – (HA2 + IH2)
= MI2 – IA2 = ( MI2 + OI2) – (IA2 + OI2)
= MO2 – OẢ2
= d2 – r2
Vậy MA.MB = d2 – r2