Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
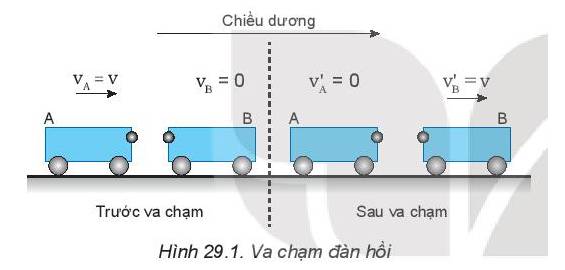
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_B' = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.{v^2}\)
2.
Từ kết quả tính được, ta thấy trong va chạm đàn hồi, động lượng được bảo toàn, năng lượng được bảo toàn.

1.
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_A' + m.v_B' = m.(v_A' + v_B') = m.\left( {\frac{v}{2} + \frac{v}{2}} \right) = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_A^{'2} + \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.\left( {\frac{{{v^2}}}{4} + \frac{{{v^2}}}{4}} \right) = \frac{1}{4}.m.{v^2}\)
2.
Từ kết quả câu 1, ta thấy trong va chạm mềm thì động lượng không thay đổi (được bảo toàn), động năng thay đổi (năng lượng không được bảo toàn).

1,
Học sinh làm thí nghiệm và so sánh kết quả.
2,
Đề xuất phương án thí nghiệm
Sử dụng điện thoại thông minh và phần mềm phân tích video để xác định được vận tốc và động lượng trước và sau va chạm của hai xe có khối lượng xác định.

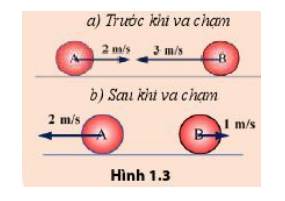
Chọn chiều dương là chiều từ trái sang phải
+ Trước khi va chạm: v1 = 2 m/s; v2 = 3 m/s
=> Động lượng của vật trước va chạm: p = m.v1 – m.v2 = m.(v1 – v2 ) = 1.(-1) = -1 (kg.m/s)
+ Sau va chạm: \(v_1' = 2\) m/s; \(v_2' = 1\) m/s
=> Động lượng của vật sau va chạm: \(p = m.( - v_1' + v_2') = 1.( - 1) = - 1(kg.m/s)\)
=> Động lượng trước va chạm = Động lượng sau va chạm
=> Kết luận: Trong quá trình chuyển động của vật, động lượng được bảo toàn

Khối lượng của hai xe là như nhau và đều có độ lớn là m = 0,245 (kg)
Động lượng của xe 1 trước va chạm: p1 = 0,444.m
Động lượng của xe 1 sau va chạm: p’1 = 0,316.m
=> Độ thay đổi động lượng của xe 1 là: \(\Delta {p_1} = \left| {p_1' - {p_1}} \right| = 0,444m - 0,316m \approx 0,03(kg.m/s)\)
Động lượng của xe 2 trước va chạm: p2 = 0,316.m
Động lượng của xe 2 sau va chạm: p’2 = 0,438.m
=> Độ thay đổi động lượng của xe 2 là: \(\Delta {p_2} = \left| {p_2' - {p_2}} \right| = 0,438m - 0,316m \approx 0,03(kg.m/s)\)
=> Độ thay đổi động lượng của xe 1 và xe 2 bằng nhau.

Động lượng của các xe trước va chạm:
+ Xe 1: \({p_1} = {m_1}.{v_1} = 0,245.0,542 \approx 0,133(kg.m/s)\)
+ Xe 2: \({p_2} = {m_2}.{v_2} = 0\)(do xe 2 đứng yên nên v2 = 0)
=> Động lượng của hệ trước va chạm là: p = 0,133 kg.m/s
Động lượng của các xe sau va chạm
+ Xe 1: \(p_1' = {m_1}.v_1' = 0,245.0,269 \approx 0,066(kg.m/s)\)
+ Xe 2: \(p_2' = {m_2}.v_2' = 0,245.0,269 \approx 0,066(kg.m/s)\)
=> Động lượng của hệ sau va chạm là: p’ = 0,132 kg.m/s
=> Động lượng của hệ trước và sau va chạm gần như bằng nhau
=> Định luật bảo toàn động lượng được nghiệm đúng.
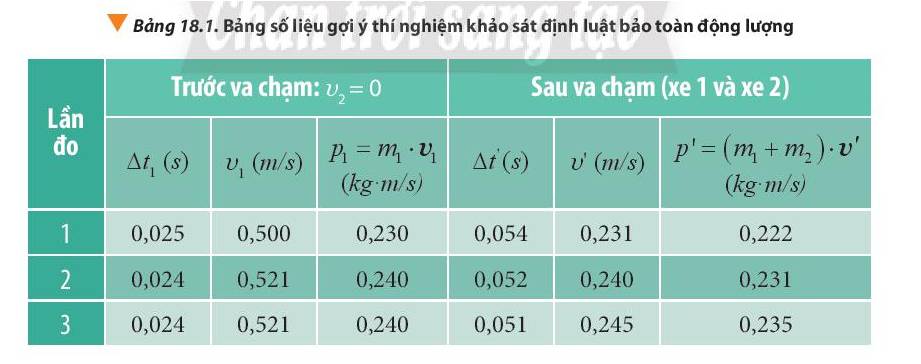
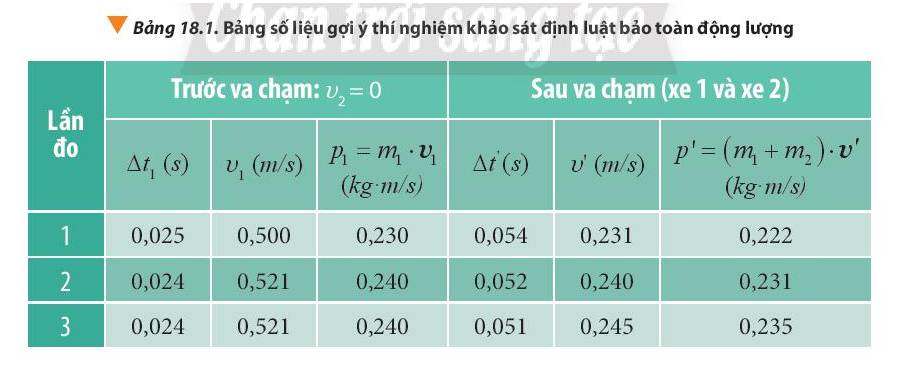


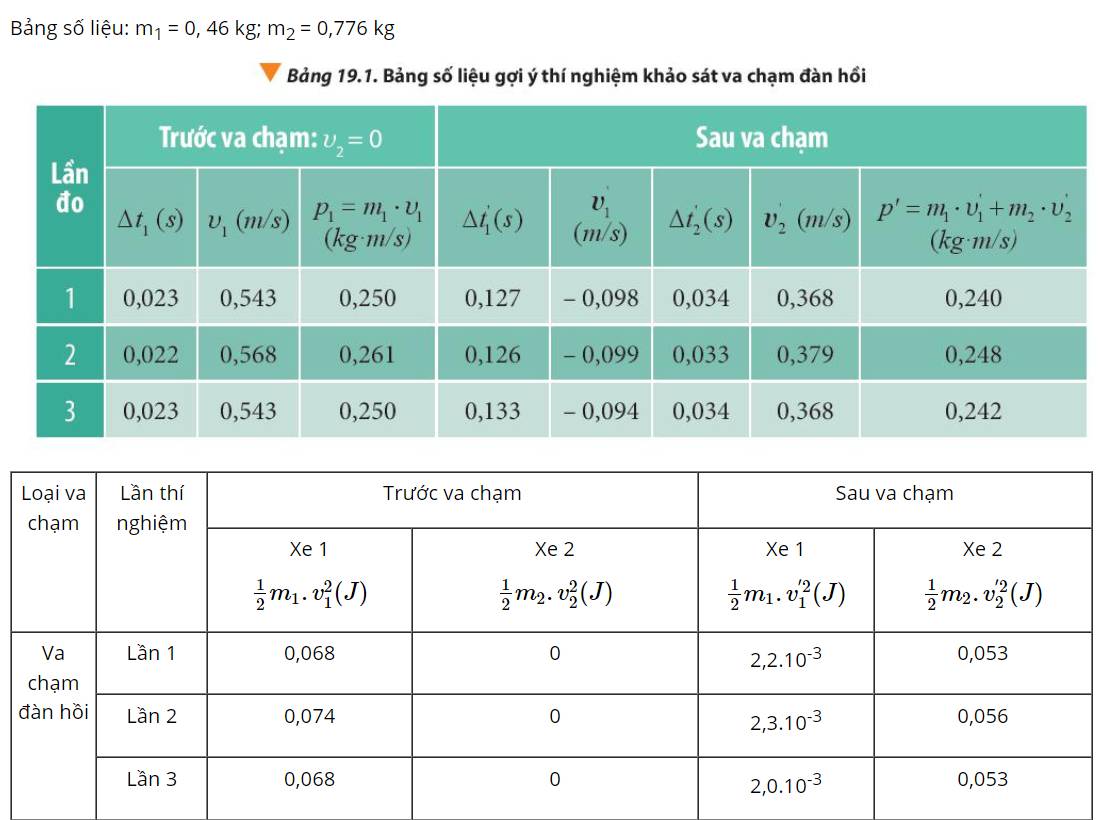
+ Lần đo 1: \(\frac{{\left| {{p_1} - p'} \right|}}{{{p_1}}}.100\% = \frac{{\left| {0,230 - 0,222} \right|}}{{0,230}}.100\% = 3,48\% \)
+ Lần đo 2: \(\frac{{\left| {{p_1} - p'} \right|}}{{{p_1}}}.100\% = \frac{{\left| {0,240 - 0,231} \right|}}{{0,240}}.100\% = 3,75\% \)
+ Lần đo 3: \(\frac{{\left| {{p_1} - p'} \right|}}{{{p_1}}}.100\% = \frac{{\left| {0,240 - 0,245} \right|}}{{0,240}}.100\% = 2,08\% \)
=> Động lượng trước và sau va chạm gần như nhau.