Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

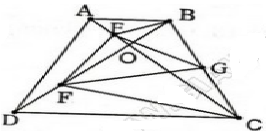
A B C D E F O G H K
Trên tia đối của ED lấy điểm K sao cho E là trung điểm của DK.
Xét \(\Delta\)DAE=\(\Delta\)KBE (c.g.c) => AD=BK (2 cạnh tương ứng)
Mà AD=BC => BK=BC => \(\Delta\)BKC cân tại B => ^BCK=(1800-^KBC)/2 (1)
Lại có: ^DAE=^KBE (2 góc tương ứng) => AD//BK (2 góc so le trg bằng nhau)
hay OH//BK => ^HOG=^KBC ( Đồng vị) (2)
E là trung điểm DK; F là trung điểm DC => EF là đường trung bình \(\Delta\)DKC
=> EF//KC hay HG//KC => ^OGH=^BCK (3)
Thay (2) và (3) vào (1); ta được: ^OGH=(1800-^HOG)/2 => \(\Delta\)HOG cân tại O
=> OG=OH (đpcm)

Xét ∆ OAD có: OE=AE; OE=FD => EF là đtb của ∆ OAD => EF=1/2AD=1/2BC (1) và EF//AD
Ta có ABCD là hình thang cân => OCDˆ=ODCˆOCD^=ODC^=60 độ ( tự lập luận)
=> ∆ ODC đều có CF là đường trung tuyến đồng thời là đường cao => CF⊥⊥BD
∆BFC vuông tại F có FG là đường trung tuyến => FG=BG=CG=BC/2( theo t/c đường trung tuyến trong ∆ vuông) (2)
Chứng minh tương tự: EG=BC/2 (3)
Từ (1) ; (2) và (3) => FG=EF=EG => ∆ EFG đều
Nhấn đúng cho mình nha ^3^
Đây là câu trả lời đầy đủ của mình
Hãy ấn đúng cho mình nha các bạn ^3^