Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F O G H K
Trên tia đối của ED lấy điểm K sao cho E là trung điểm của DK.
Xét \(\Delta\)DAE=\(\Delta\)KBE (c.g.c) => AD=BK (2 cạnh tương ứng)
Mà AD=BC => BK=BC => \(\Delta\)BKC cân tại B => ^BCK=(1800-^KBC)/2 (1)
Lại có: ^DAE=^KBE (2 góc tương ứng) => AD//BK (2 góc so le trg bằng nhau)
hay OH//BK => ^HOG=^KBC ( Đồng vị) (2)
E là trung điểm DK; F là trung điểm DC => EF là đường trung bình \(\Delta\)DKC
=> EF//KC hay HG//KC => ^OGH=^BCK (3)
Thay (2) và (3) vào (1); ta được: ^OGH=(1800-^HOG)/2 => \(\Delta\)HOG cân tại O
=> OG=OH (đpcm)

a, Vì O là trung điểm EF
MN qua O //AB//CD
=>M là trung điểm AD, N là TD BC

* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.

Câu 3:
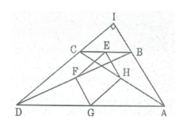
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD