Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
góc DBC=1/2*sđ cung DC=90 độ
=>DB vuông góc BC
=>DB//OA
Xét (O) có
ED,EB là tiếp tuyến
=>ED=EB
mà OD=OB
nên OE là trung trực của DB
=>OE vuông góc DB
=>OE vuông góc OA
c: Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AM*AN=AH*AO

Bài 2:
ΔOBC cân tại O
mà OK là trung tuyến
nên OK vuông góc BC
Xét tứ giác CIOK có
góc CIO+góc CKO=180 độ
=>CIOK là tứ giác nội tiếp
Bài 3:
Xét tứ giác EAOM có
góc EAO+góc EMO=180 độ
=>EAOM làtứ giác nội tiếp

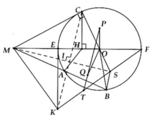
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng

E C A D B
Ta có: tỨ giác OCEA nội tiếp
=> \(\widehat{OCA}=\widehat{OEA}\)(1)
Vì OC=OB
=> Tam giác OBC cân
=> \(\widehat{OCA}=\widehat{OCB}=\widehat{OBC}\)(2)
Tứ giác ODAB nội tiếp
=> \(\widehat{ODA}=\widehat{OBC}\)( cùng bù với góc OBA) (3)
Từ (1), (2), (3)
=> \(\widehat{ODA}=\widehat{OEA}\)
=> Tam giác ODE cân có OA là đươngcao
=> OA là đường trung tuyến
=> A là trung điểm của DE

a) Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà ON là đường trung tuyến ứng với cạnh đáy AB(N là trung điểm của AB)
nên ON là đường cao ứng với cạnh AB(Định lí tam giác cân)
hay \(\widehat{ONA}=90^0\)
\(\Leftrightarrow\widehat{ONM}=90^0\)
Xét tứ giác OFMN có
\(\widehat{ONM}\) và \(\widehat{OFM}\) là hai góc đối
\(\widehat{ONM}+\widehat{OFM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OFMN là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)