Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét tứ giác BOCH có
BO//CH
OC//HB
Do đó: BOCH là hình bình hành
mà OB=OC
nên BOCH là hình thoi

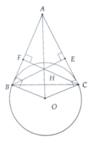
a, HS tự chứng minh
b, Chi ra rằng A,H,O cùng nằm trên đường thẳng vuông góc với BC;
c, Để H ∈ (O) thì OH = OC => C O A ^ = 60 0


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

A B C F D O I E 1 1 1
a) Xét tứ giác ABOC có: \(\widehat{ABO}=\widehat{ACO}=90^{\sigma}\left(gt\right)\Rightarrow\widehat{ABO}+\widehat{ACO}=180^{\sigma}\)
=> tứ giác ABOC nội tiếp
b) Ta có: OB = OC = R
AB = AC(tính chất 2 tiếp tuyến cắt nhau)
=> OA là đường trung trực của BC
=> BC vuông góc OA
Xét tam giác OBA và tam giác BEA có
\(\widehat{OBA}=\widehat{BEA}=90^{\sigma}\)
\(\widehat{OAB}chung\)
\(\Rightarrow\Delta OBA\)đồng dạng \(\Delta BEA\left(g.g\right)\)
\(\Rightarrow\frac{OB}{BE}=\frac{BA}{EA}\Rightarrow BA.BE=AE.BO\)
c) Xét tứ giác OIBD có \(\widehat{OID}=\widehat{OBD}=90^{\sigma}\), cùng nhìn CD
=> tứ giác OIBD nội tiếp
=> \(\widehat{IDO}=\widehat{IBO}=\frac{1}{2}sđ\widebat{IO}\left(gnt\right)\)
Mà \(\Delta OBC\)cân ( OB = OC = R) \(\Rightarrow\widehat{IBO}=\widehat{BCO}\)
\(\Rightarrow\widehat{IDO}=\widehat{BCO}\)
Chứng minh tương tự tứ giác ABOC được tứ giác OIFC nội tiếp \(\Rightarrow\widehat{OFI}=\widehat{BCO}=\frac{1}{2}sđ\widebat{OI}\left(gnt\right)\)
\(\widehat{IDO}=\widehat{OFI}\Rightarrow\Delta DOF\)cân tại O
d) Tam giác DOF cân có OI là đường cao => OI đồng thời là đường trung tuyến => ID = IF
Xét tam giác IBD và tam giác IEF có:
IB = ID ( I là trung điểm BE)
góc BID = góc EIF ( đối đỉnh)
ID = IB (cmt)
=> tam giác IBD = tam giác EIF (c.g.c)
=> góc IDB = góc IFE
=> DB // EF hay EF//AB
XÉT tam giác CBA có E là trung điểm BC và EF//AB => EF là đường trung bình của tam giác CBA
=> F là trung điểm AC
