Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là n ( Ω ) = 720 số
Gọi a b c d e f ¯ là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: 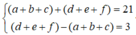
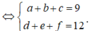
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là:
![]()

Chọn B
Gọi số cần tìm thỏa mãn điều kiện bài toán là a b c d e f ¯ trong đó a,b,c,d,e,f ∈ S và đôi một khác nhau. Theo bài ra ta có
![]()
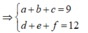
Có ![]()
![]() .
.
Ta có các cặp 3 số khác nhau từ S có tổng bằng 9 là ![]() .
.
![]()
![]()
![]()

n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20

Đáp án D.
Số cần lập có dạng
![]()
Với mỗi cách chọn 2 số từ các số đã cho ta được một số thõa mãn yêu cầu bài toán
Do đó có C 9 2 = 36 số

Đáp án D
Gọi số hạng cần tìm có dạng a → với a →
TH1: Với a = 1 => b = 2 ; 3 ; . . . ; 9 , tức là b có 8 cách chọn
TH2: Với a = 2 => b = 3 ; 4 ; . . . . . ; 9 , tức là b có 7 cách chọn
Tương tự, với các trường hợp a còn lại, tai được 8+7+.....+1 = 36 số cần tìm

Tổng 3 chữ số đầu và 3 chữ số cuối là 2+3+4+5+6+7=27, hiệu của chúng là 3
\(\Rightarrow\) Tổng 3 chữ số đầu là 12
\(\Rightarrow\) 3 chữ số đầu là (2;3;7); (2;4;6);(3;4;5) có 3 trường hợp (với mỗi bộ 3 chữ số đầu sẽ có đúng 1 bộ 3 chữ số cuối tương ứng)
\(\Rightarrow\) Có \(3.3!.3!=108\) số thỏa mãn

Đáp án B
Số cần lập là a b c d e f , ta có a + b + c – 1 = d + e + f <=> 20 = 2(d + e + f) <=> d + e + f = 10
Với mỗi f ∈ { 1 ; 3 ; 5 } => d, e có 4 cách chọn, suy ra a b c d e f có 4.3! = 24 cách chọn
Suy ra có 3.24 = 72 số có thể lập thỏa mãn đề bài.




Gọi tổng của 3 chữ số hàng đơn vị, chục, trăm là x và tổng 3 chữ số còn lại là y
\(\Rightarrow\left\{{}\begin{matrix}x+y=1+2+3+4+5+6=21\\x-y=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=12\\y=9\end{matrix}\right.\)
Do đó ta có các bộ (đơn vị, chục, trăm) là \(\left(1;5;6\right);\left(2;4;6\right);\left(3;4;5\right)\) có 3 bộ, tương ứng mỗi bộ là 3 chữ số còn lại ở các hàng ngàn, chục ngàn, trăm ngàn
Do đó số chữ số thỏa mãn là: \(3.\left(3!\right)^2=108\)