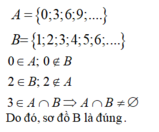Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Dựa vào các bước chứng minh ta thấy lập luận đó là chính xác tất cả các bước.

1) \(a^5-a=a\left(a^4-1\right)=a\left(a^2-1\right)\left(a^2+1\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4+5\right)\)
\(=\left(a-1\right)a\left(a+1\right)\left(a^2-4\right)+5\left(a-1\right)a\left(a+1\right)\)
\(=\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)+5\left(a-1\right)a\left(a+1\right)⋮5\)
Vì \(\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)⋮5\)( tích 5 số nguyên liên tiếp chia hết cho 5)
và \(5\left(a-1\right)a\left(a+1\right)⋮5\)
=> \(a^5-a⋮5\)
Nếu \(a^5⋮5\)=> a chia hết cho 5

a) Không thể khẳng định câu trên là đúng hay sai.
b)
+) n = 0 hoặc n =5 thì “n chia hết cho 5” là khẳng định đúng.
+) n = 2 hoặc n =34 thì “n chia hết cho 5” là khẳng định sai.


Có tất cả 99 số nguyên dương nhỏ hơn 100.
Số cách chọn một tập hợp gồm hai trong 99 số đó là: \(C_{99}^2 = 4851\)
Số cách chọn một tập hợp gồm ba số trong 99 số đó là: \(C_{99}^3 = 156849\)