Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) Gọi p là số proton của nguyên tố X
Đồng vị X1 có 3 loại hạt bằng nhau nên 3p = 18 suy ra p = 6
Đồng vị X2 có tổng số hạt 20 nên 2p + n’ = 20 suy ra n’ = 8
Số khối của các đồng vị X1, X2 lần lượt là 12, 14
Phần trăm hai đồng vị bằng nhau suy ra mỗi đồng vị chiếm 50%
Atb = (12.50 + 14.50) / 100 = 13 đvC
b)
Gọi số khối của hai đồng vị X, Y là A1 và A2; phần trăm số nguyên tử của hai đồng vị này là x1 và x2. Theo giả thiết ta có:
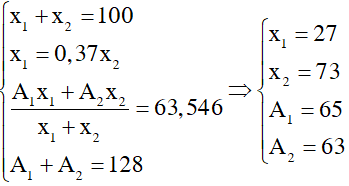
1
a , các loại hạt trong X1 bằng nhau <=> p=n1=e=6 (hạt) => A1 = 12
=> n2 = 20-6.12=8(hạt) => A2 = 8+6=14
%X1 = %X2 = 50%
\(\overline{\text{A}}=\frac{14.50+12.50}{100}=13\)
2 , gọi 2 đồng vị A1p Y và A2p Z , phần trăm của 2 đồng vị lần lượt la x1 , x2
Theo bài ra
A1 + A2 =128
x1 + x2 = 100
\(\overline{M}=\frac{A_1x_1+A_2x_2}{100}=\) 63,54
x1 - 0,37x2 = 0
=> A1 = 65 , A2 = 63

Ta có: Nguyên tử oxygen có số hiệu nguyên tử Z = 8
Mà số hiệu nguyên tử thỏa mãn \(1 \leqslant \frac{N}{Z} \leqslant 1,25\) thì bền vững
Thay Z vào bất phương trình \(1 \leqslant \frac{N}{Z} \leqslant 1,25\) ta được:
\(1 \leqslant \frac{N}{8} \leqslant 1,25\)
=> \(8 \leqslant N \leqslant 10\)
=> \(8 + Z \leqslant N + Z \leqslant 10 + Z\)
=> \(16 \leqslant A \leqslant 18\)
Vậy các đồng vị thường gặp của oxygen là: \({}_8^{16}O\), \({}_8^{17}O\), \({}_8^{18}O\).

Từ \(^{16}_8O\) có: \(^1_1H^1_1H^{16}_8O\), \(^2_1H^2_1H^{16}_8O\) và \(^1_1H^2_1H^{16}_8O\)
Từ \(^{17}_8O\) có: \(^1_1H^1_1H^{17}_8O\), \(^2_1H^2_1H^{17}_8O\) và \(^1_1H^2_1H^{17}_8O\)
Từ \(^{18}_8O\) có: \(^1_1H^1_1H^{18}_8O\), \(^2_1H^2_1H^{18}_8O\) và \(^1_1H^2_1H^{18}_8O\)
→ Vậy có 9 loại phân tử nước có thành phần đồng vị khác nhau.

Bài 1:
Gọi x là số khối của đồng vị thứ 2, ta có:
\(\frac{107.56\%+x44\%}{100\%}=107,88\)
\(\Rightarrow x=109\)
Vậy số khối của đồng vị thứ 2 là 109
Nếu có 500 nguyên tử Ag thì số nguyên tử của đồng vị thứ 2 là: \(\frac{44\%.500}{100\%}=220\) (nguyên tử)
\(M_{Ag^{ }_2O}=\left(107,88.2\right)+16=231,76\)
\(\Rightarrow n=\frac{57,94}{231,76}=0,25\left(mol\right)\)
Xét trong 1 mol Ag2O có \(\begin{cases}2molAg\\1molO\end{cases}\)
\(\Rightarrow\) trong 0,25 mol Ag2O có 0,5 mol Ag
\(\Rightarrow\) trong 0,5 mol Ag có \(\frac{56\%.0,5}{100\%}=0.28\left(mol\right)\) đồng vị 107Ag
\(\Rightarrow m_{^{107}Ag}\) = 107 . 0,28 = 29,96 (gam)
Bài 2:
a) Gọi x, y lần lượt là % về số nguyên tử của 2 đồng vị 35Cl và 37Cl, ta có:
\(\begin{cases}x+y=100\\\frac{35x+37y}{100}=35,5\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}x=75\\y=25\end{cases}\)
Vậy đồng vị 35Cl chiếm 75%; đồng vị 37Cl chiếm 25%
b) Tính % về gì vậy bạn?
c) \(M_{AlCl_3}\) = 27 + (35,5 .3) = 133,5
\(\Rightarrow n_{AlCl_3}\) = \(\frac{13,35}{133,5}=0,1\left(mol\right)\)
Xét trong 1 mol AlCl3 có \(\begin{cases}1molAl\\3molCl\end{cases}\)
=> trong 0,1 mol AlCl3 có 0,3 mol Cl
=> trong 0,3 mol Cl có \(\frac{75\%.0,3}{100\%}=0,225\left(mol\right)\) đồng vị 35Cl
=> Số nguyên tử 35Cl có trong 13,35g AlCl3 là:
0,225 . 6,02 . 1023 = 1,3545.1023 (nguyên tử)
1)Cách 1: nhẩm nhanh cho các bài có Z nhỏ, Z lớn vẫn có thể áp dụng nếu bạn gần như đã thuộc bảng tuần hoàn-để có thể suy ra đáp án :d) lấy 10/3 xấp xỉ 3,333 => lấy số gần nhất là 3 tương đương với Z của Nguyên tử cần tìm => Li (giải thích: tổng 3 hạt là E,N,P trong đó E P bằng nhau(, N thì lớn hơn hoặc bằng P, nên muốn tìm Z (Z = E =P) thì chia 3 ra (3 hạt), lấy số đó hoặc phần nguyên nếu lẻ), Z nhỏ thì NP không khác nhau nhiều, còn Z lớn ví dụ (Fe Z=26, N=30, tổng số hạt là 82 chia 3 ra thì là 27,333...không còn đúng nữa.!
Cách 2: cách chính quy dùng cho Kt trên lớp, kiếm điểm:D:
3≤ (2Z+N)/Z < 3,5 (*)=> 2,8...<Z<3,33... => Z=3 (Li) cách này áp dụng cho mọi bài tập dạng này. để hiểu rõ hơn vì sao có công thức (*) bạn nghiên cứu thêm bài tập 1.19 trong sách bài tập hóa lớp 10 trang 6.
2)Mtb= 109*44%+X*(100-44)%=107,88 => X=107

Tỉ lệ mỗi đồng vị O trong hỗn hợp 3 đồng vị:
99,757% 16O => 99757 nguyên tử 16O
0,039% 17O => 39 nguyên tử 17O
0,204% 18O => 204 nguyên tử 18O
Khi có một nguyên tử 17O thì số nguyên tử:
16O là: 99757399975739 = 2558 nguyên tử.
18O là: 2042920429 = 5 nguyên tử.

Tỉ lệ mỗi đồng vị O trong hỗn hợp 3 đồng vị:
99,757% 16O => 99757 nguyên tử 16O
0,039% 17O => 39 nguyên tử 17O
0,204% 18O => 204 nguyên tử 18O
Khi có một nguyên tử 17O thì số nguyên tử:
16O là: 99757399975739 = 2558 nguyên tử.
18O là: 2042920429 = 5 nguyên tử.
Ta có: \(\left\{{}\begin{matrix}x_1+x_2+x_3=100\\x_1=15x_2\\x_1-x_2=21x_3\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x_1=90\%\\x_2=6\text{% }\\x_3=4\%\end{matrix}\right.\)
\(\Rightarrow\overline{A_O}\)
dễ vậy mà ko nghĩ ra