Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có 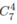 cách.
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có 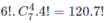 cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có 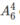 cách.
cách.
Theo quy tắc nhân, có 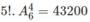 cách.
cách.

Xếp 2 bạn nữ đứng trước, số cách là 2!.
Sau đó chọn 2 bạn nam chen vào giữa 2 bạn nữ, số cách chọn; xếp 2 bạn nam đó là ![]() .
.
Sau khi chọn 2 bạn nam đó rồi thì còn 6 bạn nam. Ta coi 2bạn nam và 2 bạn nữa đã xếp chỗ là 1 bạn cùng với 6 bạn nam chưa xếp là có 7 bạn.
Số cách xếp 7 bạn này là 7!.
Áp dụng quy tắc nhân; số cách xếp tất cả là: ![]()
Chọn B.

Số cách xếp là:
\(\left(C^2_4\cdot C^2_4-2!\cdot2!\cdot2!\right)\cdot2=56\left(cách\right)\)

\(A:\)"Không có 2 nữ ngồi cạnh nhau"
Xếp sao cho không có 2 bạn nữ nào ngồi cạnh nhau tức nam nữ ngồi xen kẽ.
Xếp 7 bạn nam có \(7!\) cách xếp.
Giữa 7 bạn nam có 8 khoảng trống(gồm 6 khoảng trống ở giữa và 2 khoảng trống ở đầu và cuối)
Xếp 5 bạn nữ sao cho không có 2 bạn nữ nào ngồi cạnh nhau ta xếp 5 bạn nữ vào 2 trong 8 khoảng trống đó có \(A_8^5\)cách xếp.
\(\Rightarrow n\left(A\right)=7!\cdot A_8^5\) cách xếp.

👍🏻 Cách 1.
Như trên hình là số thứ tự các ghế
❤️ Trường hợp 1
Ghế có số lẻ là ghế các bạn nữ thì
G1 có 4 lựa chọn
G3 có 3 lựa chọn
G5 có 2 lựa chọn
G1 có 1 lựa chọn
Các ghế chẵn là nam
G2 có 4 lựa chọn
G4 có 3 lựa chọn
G6 có 2 lựa chọn
G8 có 1 lựa chọn
==> Với trường hợp 1 sẽ có
(4x3x2x1)x(4x3x2x1)=576 cách xếp
❤️ Trường hợp 2
Các ghế lẻ là nam và các ghế chẵn là nữ thì tương tự ta cũng có 576 cách xếp
=> Với cách 1 ta có
2x576=1152 cách xếp
Cách 2 xếp 2 bàn ngược lại với cách 1 thì ta cũng sẽ có
1152 cách xếp
=> Với 2 cách xếp + 4 trường hợp ta có
2x1152=2304 cách xếp
