Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại điểm M cho vân sáng \(\Rightarrow x_M=ki=k\dfrac{\lambda D}{a}\)
\(\Rightarrow 1,2=k\dfrac{\lambda .2}{4}\)
\(\Rightarrow \lambda = \dfrac{2,4}{k}\)
\(0,4\le \lambda \le 0,75\)
\(\Rightarrow 3,2\le k\le6\)
Suy ra:
\(\lambda_{min}=\dfrac{2,4}{6}=0,4\mu m\)
\(\lambda_{max}=\dfrac{2,4}{4}=0,6\mu m\)

Chọn B
Ta có:
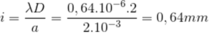
số vân sáng quan sát được trên vùng giao thoa đối xứng là:
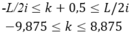
=> Có 18 giá trị của k thỏa mãn
Vậy trên màn có 18 vân tối

Câu 18.
a)Bề rộng của 16 vân sáng là \(15i\) \(\Rightarrow15i=18\Rightarrow i=1,2mm\)
Khoảng vân: \(i=\dfrac{\lambda D}{a}\)
Khoảng cách từ hai khe đến màn:
\(D=\dfrac{a\cdot i}{\lambda}=\dfrac{1,2\cdot10^{-3}\cdot1,2\cdot10^{-3}}{0,6\cdot10^{-6}}=2,4m\)
b) Bề rộng quan sát 21 vân sáng là \(20i'\Rightarrow\) \(20i'=18\Rightarrow i'=0,9mm\)
Bước sóng: \(\lambda'=\dfrac{a\cdot i'}{D}=\dfrac{1,2\cdot10^{-3}\cdot0,9\cdot10^{-3}}{2,4}=0,45\cdot10^{-6}\left(m\right)=0,45\mu m\)
c)Tại vị trí cách vân trung tâm 6mm: \(x=6i\)
\(\Rightarrow\)Vân sáng bậc 6.
Câu 19.
Vân tối thứ 5 của hệ ứng với \(\lambda_1\) trùng với vân sáng bậc 5 của hệ vân ứng với \(\lambda_2\).
\(\Rightarrow5,5i_1=5i_2\)
\(\Rightarrow5,5\cdot\dfrac{\lambda_1\cdot D}{a}=5\cdot\dfrac{\lambda_2\cdot D}{a}\)
\(\Rightarrow5,5\lambda_1=5\lambda_2\)
\(\Rightarrow\lambda_2=\dfrac{5,5\cdot0,6}{5}=0,66\mu m\)
Câu 20.
Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,55\cdot10^{-6}\cdot1,8}{1,1\cdot10^{-3}}=9\cdot10^{-4}\left(m\right)\)
Khoảng vân mới: \(i'=1,2i=1,2\cdot9\cdot10^{-4}=1,08\cdot10^{-3}\left(m\right)\)
Bước sóng mới: \(\lambda'=\dfrac{a\cdot i'}{D}=\dfrac{1,1\cdot10^{-3}\cdot1,08\cdot10^{-3}}{1,8}=0,66\cdot10^{-6}\left(m\right)=0,66\mu m\)
Câu 21.
Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,6\cdot10^{-6}\cdot2}{2\cdot10^{-3}}=6\cdot10^{-7}\left(m\right)\)
Số vân sáng quan sát được: \(N=\dfrac{25,8\cdot10^{-3}}{6\cdot10^{-7}}=43000\)

\(x_M=3i=3.0,2=0,6mm\)
Khi thay \(\lambda\) bởi \(\lambda'\) thì tại M cũng là vân sáng
\(x_M=ki\) (k < 3)
\(\Rightarrow 0,6=k\dfrac{\lambda' .1}{2}\)
\(\Rightarrow \lambda' = \dfrac{1,2}{k}\)
Vì \(\lambda'\) cho vân sáng nên k = 2 (k = 1 thì \(\lambda'=1,2\mu m\) là bức xạ hồng ngoại)
\(\Rightarrow \lambda'=o,6 \mu m\)

Đáp án B
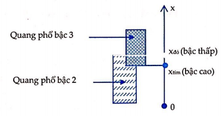
Trong giao thoa ánh sáng trắng thì hai bên vân sáng trung tâm có các dải quang phổ liên tục “tím ở trong, đỏ ở ngoài” gọi là quang phổ. Quang phổ bậc 2 và bậc 1 cách nhau một khe đen nhưng quang phổ bậc 3 thì chồng lên quang phổ bậc 2. Bề rộng vùng phủ nhau giữa quang phổ bậc hai và bậc ba là:
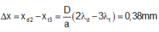

Bước sóng: \(i = \dfrac{\lambda D}{a}=\dfrac{0,5. 2}{0,5}=2mm\)
Số vân tối quan sát được là: \(2.|\dfrac{12}{2}+0,5|=12\)
Trong trường hợp trường giao thoa đối xứng
Công thức tìm số vân sáng: \(|\dfrac{Bề-rộng-trường-giao-thoa}{2.i}| .2 +1\)
Công thức tìm số vân tối: \(|\dfrac{Bề-rộng-trường-giao-thoa}{2.i}+0,5| .2\)
Trong đó, |là lấy phần nguyên|
Ví dụ: \(|9,1|=9\)
\(|9,9|=9\)

\(i_1=\dfrac{\lambda_1 D}{a}=0,38mm\)
\(i_2=\dfrac{\lambda_2 D}{a}=0,76mm\)
Ta thấy \(2i_1=i_2\) nên quang phổ bậc 2 sát với quang phổ bậc 1.
Do vậy, vùng tối trên màn chỉ từ vân trug tâm đến vạch đỏ đầu tiên, rộng là: \(2.i_1=0,76mm\)