Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Ta có: AB→AB→= (4,-3)
AC→AC→= (12,-9)
412412=−3−9−3−9 \Rightarrow 3 điểm A, B, C thẳng hàng
b) Tọa độ điểm D(xDxD,yDyD)
A là trung điểm BD \Rightarrow xAxA=xD+xB2xD+xB2
\Rightarrow xDxD= -7
Tương tự, yDyD= 7
Vậy tọa độ D(-7,7)
c)Tọa độ điểm E(xExE,0)
AE→AE→= xExE+3, -4)
A, B,E thẳng hàng \Rightarrow xExE= ?!? (Áp dụng tương tự câu a)
BàI 1:a) Để 3 điểm A,B,C thẳng hàng tì ta xét tỉ số, chúng = nhau suy ra A,B,C thẳng hàng(xét tỉ số giữa hoành độ của vecto AB vs AC so vs tung độ của vecto AB vs AC)
b)Theo công thức trung điểm thì sẽ tìm được tọa độ điểm D
c)Điểm E thuộc Ox thì E(xE,0).Mà 3 điểm A,B,E thẳng hàng nên xét tỉ số ta có : 4/xE+3 bằng -3/-4.Vậy tọa độ điểm E (7/3,0)
Bài 2:a)tho công thức trộng tâm trong SGK thì ta tính được tọa độ là(0,1)
b)ta có xC=1/3(xA+xB+xD), yC=1/3(yA+yB+yD).Vậy tọa độ điểm D(8,-11)
c) Để ABCE là hbh thì vecto AB= vecto EC nên ta có xAB=xEC,yAB=yEC.Vậy tọa độ của điểm E(-4,-5)
Bài 3:a)Ta xét tỉ số giữ 2 vecto AB và AC thấy chung khác nhau nên A,B,C không thẳng hàng.
b) vecto AD=3 vecto BC suy ra xD-xA=3(xC-xB),yD-yA=3(yC-yB).Vậy tọa độ điểm D(21,-14)
c) Điểm O(0,0). Do E là trọng tâm tam giác ABE nên: 0=1/3(xA+xB+xE),0=1/3(yA+yB+yE).Vậy E (2,-5)

a) Ta thấy \(\overrightarrow{AB}\left(3;2\right)\) và \(\overrightarrow{AC}\left(4;-3\right)\). Vì \(\dfrac{3}{4}\ne\dfrac{2}{-3}\) nên A, B, C không thẳng hàng.
b) Ta có \(\overrightarrow{BC}\left(1;-5\right)\)
Do vậy \(AB=\left|\overrightarrow{AB}\right|=\sqrt{3^2+2^2}=\sqrt{13}\)
\(AC=\left|\overrightarrow{AC}\right|=\sqrt{4^2+\left(-3\right)^2}=5\)
\(BC=\left|\overrightarrow{BC}\right|=\sqrt{1^2+\left(-5\right)^2}=\sqrt{26}\)
\(\Rightarrow C_{ABC}=AB+AC+BC=5+\sqrt{13}+\sqrt{26}\)
c) Gọi M, N, P lần lượt là trung điểm BC, CA, AB.
\(\Rightarrow P=\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)=\left(-\dfrac{3}{2};3\right)\)
\(N=\left(\dfrac{x_A+x_C}{2};\dfrac{y_A+y_C}{2}\right)=\left(-1;\dfrac{1}{2}\right)\)
\(M=\left(\dfrac{x_B+x_C}{2};\dfrac{y_B+y_C}{2}\right)=\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
d) Gọi G là trọng tâm tam giác ABC thì \(G=\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(-\dfrac{2}{3};\dfrac{5}{3}\right)\)
e) Gọi \(D\left(x_D;y_D\right)\) là điểm thỏa mãn ycbt.
Để ABCD là hình bình hành thì \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left(3;2\right)=\left(1-x_D;-1-y_D\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3=1-x_D\\2=-1-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-2\\y_D=-3\end{matrix}\right.\)
\(\Rightarrow D\left(-2;-3\right)\)
f) Bạn xem lại đề nhé.

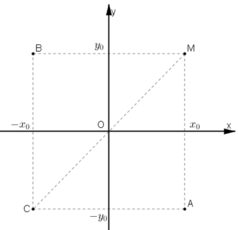
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
