Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(PT\left(T\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\)
\(\left\{{}\begin{matrix}A\left(-1;2\right)\in\left(T\right)\\B\left(1;2\right)\in\left(T\right)\\C\left(2;-3\right)\in\left(T\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2+2^2+2a-4b+c=0\\1^2+2^2-2a-4b+c=0\\2^2+\left(-3\right)^2-4a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-4b+c=-5\\-2a-4b+c=-5\\-4a+6b+c=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-\dfrac{4}{5}\\c=-\dfrac{41}{5}\end{matrix}\right.\)
\(\Rightarrow\)Tâm \(I\left(0;-\dfrac{4}{5}\right)\)

Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)

\(AB^2=\left(1+1\right)^2+\left(2-0\right)^2=8\)
\(AC^2=\left(5+1\right)^2+\left(-2-0\right)^2=39\)
\(BC^2=\left(5-1\right)^2+\left(-2-2\right)^2=32\)
Cạnh lớn nhất là AC, ta có:
AC2 < AB2 + BC2
=> Tam giác ABC nhọn
A B 5 1 2 -2 C D E F
Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE)
= 5.4 - 4.4/2 - 5.1/2 - 3.1/2
= 8
Gọi H(x,y), ta có BH vuông góc với AC => \(\overrightarrow{BH}.\overrightarrow{AC}=0\) => (x - 1).(5-0) + (y - 2)(-2 +1) = 0
=> 5x - y = 3 (1)
Phương trình đt AC là: \(\frac{y+1}{-2+1}=\frac{x-0}{5-0}\) => 5y + x = -5
Vì H thuộc AC nên 5y + x = -5 (2)
Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13
Vậy H(5/13; -14/13)
AB2=(1+1)2+(2−0)2=8
AC2=(5+1)2+(−2−0)2=39
BC2=(5−1)2+(−2−2)2=32
Cạnh lớn nhất là AC, ta có:
AC2 < AB2 + BC2
=> Tam giác ABC nhọn
AB512-2CDEF
Diện tích ABC= dt(CDEF) - dt(CDB) - dt(CFA) - dt(ABE)
= 5.4 - 4.4/2 - 5.1/2 - 3.1/2
= 8
Gọi H(x,y), ta có BH vuông góc với AC => BH−→−−.AC−→−−=0 => (x - 1).(5-0) + (y - 2)(-2 +1) = 0
=> 5x - y = 3 (1)
Phương trình đt AC là: y+1−2+1=x−05−0 => 5y + x = -5
Vì H thuộc AC nên 5y + x = -5 (2)
Từ (1) và (2), giải hệ pt ta có: x =5/13 và y = -14/13
Vậy H(5/13; -14/13)

Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.

\(\overrightarrow{AB}=\left(1;-5\right)\)
Do \(\Delta\) vuông góc AB nên \(\Delta\) nhận \(\left(1;-5\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(x-5y+c=0\) (với c khác 0 do \(\Delta\) tạo với 2 trục tọa độ 1 tam giác)
Giao điểm A của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\x-5y+c=0\end{matrix}\right.\) \(\Rightarrow A\left(-c;0\right)\) \(\Rightarrow OA=\left|c\right|\)
Giao điểm B của \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\x-5y+c=0\end{matrix}\right.\) \(\Rightarrow B\left(0;\frac{c}{5}\right)\) \(\Rightarrow OB=\left|\frac{c}{5}\right|\)
\(S_{OAB}=10\Leftrightarrow\frac{1}{2}OA.OB=10\Leftrightarrow OA.OB=20\)
\(\Leftrightarrow\left|c\right|.\left|\frac{c}{5}\right|=20\Leftrightarrow c^2=100\Rightarrow\left[{}\begin{matrix}c=10\\c=-10\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x-5y+10=0\\x-5y-10=0\end{matrix}\right.\)
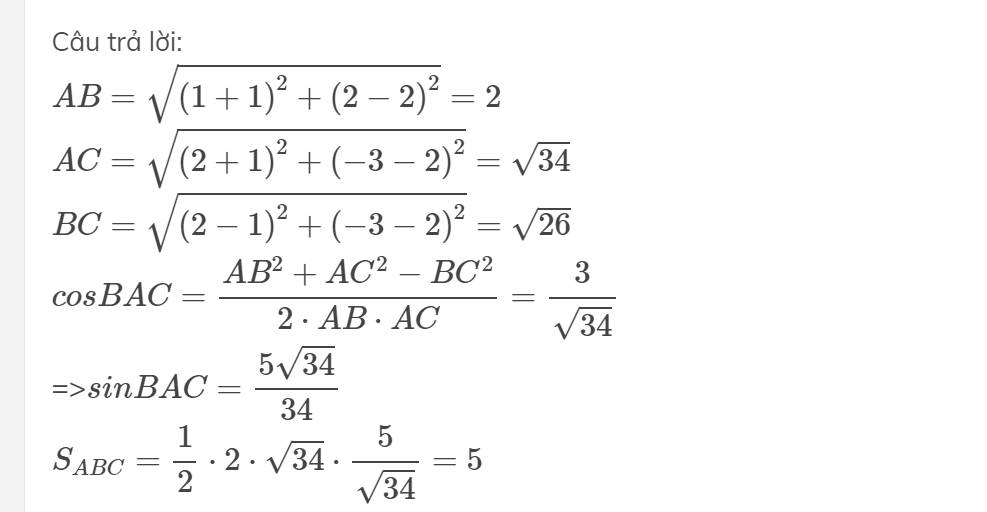
\(AB=\sqrt{\left(1+1\right)^2+\left(2-2\right)^2}=2\)
\(AC=\sqrt{\left(2+1\right)^2+\left(-3-2\right)^2}=\sqrt{34}\)
\(BC=\sqrt{\left(2-1\right)^2+\left(-3-2\right)^2}=\sqrt{26}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{3}{\sqrt{34}}\)
=>\(sinBAC=\dfrac{5\sqrt{34}}{34}\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\cdot\sqrt{34}\cdot\dfrac{5}{\sqrt{34}}=5\)