Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phép tịnh tiến biến(d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương v → của (d) : v → ( 2019 ; − 2018 ) = k u → = 0 ; k m =>m = 0
=>có một giá trị m = 0 để biến (d) thành chính nó

Đáp án B
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → 2 k ; k m =>k 2019 2 => m = − 4046 2019
=>có một giá trị m = − 4046 2019 để biến (d) thành chính nó

Đáp án D
Để biến d thành chính nó, ta tịnh tiến d theo VTCP của nó.

15.
Gọi $\overrightarrow{v}=(a,b)$
Theo bài ra ta có:
$T_{\overrightarrow{v}}(B)=A$
$\Leftrightarrow \overrightarrow{BA}=\overrightarrow{v}$
$\Leftrightarrow (-4,4)=\overrightarrow{v}$
4.
Bạn nhớ tính chất sau: phép tịnh tiến theo vecto $\overrightarrow{v}$ biến đường thẳng thành chính nó khi và chỉ khi $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng $d$.
Dễ thấy $\overrightarrow{u_d}=(1,2)$ nên $\overrightarrow{v}=(1,2)$. Đáp án C.
Giải theo cách thuần thông thường:
Gọi vecto cần tìm là $\overrightarrow{v}=(a,b)$
Gọi $M(x,2x+1)$ là điểm thuộc đường thẳng $d$
$M'(x',y')=T_{\overrightarrow{v}}(M)\in (d)$
\(\Rightarrow \left\{\begin{matrix} x'=x+a; y'=2x+1+b\\ 2x'-y'+1=0\end{matrix}\right.\)
\(\Rightarrow 2(x+a)-(2x+1+b)+1=0\)
\(\Leftrightarrow 2a=b\)
Vậy $\overrightarrow{v}=(1,2)$

4.
Để phép tịnh tiến theo \(\overrightarrow{v}\) biến d thành chính nó thì \(\overrightarrow{v}\) phải là 1 vecto chỉ phương của d
Khi đó \(\overrightarrow{v}=k\left(1;2\right)\) với k là số thực
5.
Đường tròn tâm \(I\left(2;1\right)\) bán kính \(R=4\)
Phép tịnh tiến theo \(\overrightarrow{v}\) biến đường tròn thành đường tròn tâm I' bán kính R=4
\(I'=T_{\overrightarrow{v}}\left(I\right)\Rightarrow\left\{{}\begin{matrix}x_{I'}=2+1=3\\y_{I'}=3+1=4\end{matrix}\right.\) \(\Rightarrow I'\left(3;4\right)\)
Phương trình đường tròn: \(\left(x-3\right)^2+\left(y-4\right)^2=16\)

4.
Phép tịnh tiến vecto v biến d thành chính nó khi v cùng phương với vecto chỉ phương của d
Ta có \(\left(1;2\right)\) là 1 vtcp của d
Do đó vecto \(\overrightarrow{v}=\left(k;2k\right)\) với k là 1 số thực nào đó
22.
B là ảnh của C qua phép tịnh tiến vecto DA
26.
Không tồn tại phép tịnh tiến biến hình vuông thành chính nó (nếu ko kể phép tịnh tiến theo vecto-không)
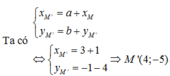
Đáp án A
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → = 2019 k ; k m => k = 1 m = – 2018
=>có một giá trị m = – 2018 để biến (d) thành chính nó