Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số câu hỏi được trả lời đúng ở vòng sơ tuyển (x nguyên dương)
Số câu hỏi trả lời sai: 10 – x
Số điểm người dự thi đạt được: 10 + 5x – (10 -x)
Người dự thi muốn thi tiếp vòng sau thì 10 + 5x – (10 -x) ≥ 40
⇔ 6x ≥ 40 ⇔ x ≥ 20/3. Do x nguyên dương nên x ∈ {7;8;9;10}

Gọi số học sinh toàn trường đầu năm học là a học sinh (a ∈ N*)
Số học sinh nữ đầu năm học là a/ 2 học sinh.
Khi nhà trường nhận thêm 15 học sinh nữ và 5 học sinh nam thì số học sinh nữ là a/2 + 15 và số học sinh toàn trường là a + 20 học sinh.
Vì số học sinh nữ lúc này chiếm 51% số học sinh toàn trường nên ta có phương trình:
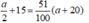
⇔ 50a + 1500 = 51a + 1020
⇔ a = 480 (thỏa mãn điều kiện a ∈ N*)
Vậy đến cuối kì I số học sinh nữ trong trường là 480: 2 + 15 = 255 học sinh, số học sinh nam là 480: 2 + 5 = 245 học sinh.

gọi a,b,c lần lượt là số học sinh chỉ giải được bài A,B,C
d là số học sinh giải được 2 bài B và C nhưng không giải được bài A
Khi đó : số học sinh giải được bài A và thêm ít nhất 1 bài trong hai bài B và C là : 25 - a - b - c - d
Theo bài ra :
Số thí sinh chỉ giải được bài A bằng số thí sinh chỉ giải được bài B cộng với số thí sinh chỉ giải được bài C
\(\Rightarrow a=b+c\)
số thí sinh không giải được bài A thì số thí sinh đã giải được bài B gấp hai lần số học sinh giải được bài C
\(\Rightarrow b+d=2\left(c+d\right)\)
Số học sinh chỉ giải được bài A nhiều hơn số thí sinh giải được bài A và thêm bài khác là một người
\(\Rightarrow\) a = 1 + 25 - a - b - c - d
từ các đẳng thức trên suy ra : \(\hept{\begin{cases}b=2c+d\\3\left(b+c\right)=26-d\end{cases}\Rightarrow\hept{\begin{cases}d=b-2c>0\\3\left(b+c\right)+b-2c=26\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}d=b-2c>0\\4b+c=26\end{cases}\Rightarrow\hept{\begin{cases}b=6\\c=2\end{cases}}}\)
Vậy ....

- Số học sinh vượt qua vòng 1 là : \(30\%.400=120\) ( học sinh )
- Số học sinh nữ vượt qua vòng 1 là : \(\frac{\left(400-220\right)}{3}=60\) ( học sinh )
-> Số học sinh nam vượt qua vòng 1 là : \(120-60=60\) ( học sinh )
- Phàn trăm học sinh nam vượt qua vòng 1 là : \(\frac{60}{220}.100\%\approx27,27\%\)