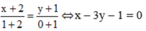Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ A1 là ảnh của A qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_{A_1}=x_A=-1\\y_{A_1}=-y_A=-2\end{matrix}\right.\)
Vậy: \(A_1\left(-1;-2\right)\)
b: Tọa độ A2 là ảnh của A qua phép đối xứng trục Oy là:
\(\left\{{}\begin{matrix}x_{A_2}=-x_A=1\\y_{A_2}=y_A=2\end{matrix}\right.\)
Vậy: \(A_2\left(1;2\right)\)
c: Tọa độ giao điểm B của (Δ) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-y-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Vậy: B(1/2;0)
Vì B thuộc Ox nên phép đối xứng qua trục Ox biến B thành chính nó
Lấy C(1;1) thuộc (d)
Tọa độ D là ảnh của C qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_D=x_C=1\\y_D=-y_C=-1\end{matrix}\right.\)
Vậy: D(1;-1)
Do đó: Δ' là phương trình đường thẳng đi qua hai điểm B(1/2;0); D(1;-1)
\(\overrightarrow{BD}=\left(\dfrac{1}{2};-1\right)=\left(1;-2\right)\)
=>VTPT là (2;1)
Phương trình Δ' là:
\(2\left(x-1\right)+1\left(y+1\right)=0\)
=>2x-2+y+1=0
=>2x+y-1=0

Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2.3+4.1+5\right|}{\sqrt{3^2+4^2}}=\frac{15}{5}=3\)

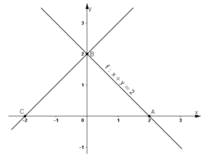
* Ta có A(2; 0) thuộc tia Ox.
Gọi Q(O,90º) (A) = B thì B thuộc tia Oy và OA = OB nên B(0 ; 2).
* Gọi d’ là ảnh của d qua phép quay tâm O, góc quay 90º.
+ A(2 ; 0) ∈ (d)
⇒ B = Q(O,90º) (A) ∈ (d’)
+ B(0 ; 2) ∈ (d).
⇒ C = Q(O,90º) (B) ∈ (d’).
Dễ dàng nhận thấy C(-2; 0) (hình vẽ).
⇒ (d’) chính là đường thẳng BC.
Đường thẳng d’ đi qua B(0 ; 2) và C(-2; 0) nên có phương trình đoạn chắn là:
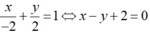

Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
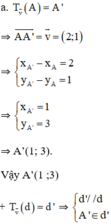
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :