Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\left(d\right):y=ax+b\) song song với \(\left(d\right):y=3x-1\)
\(\Rightarrow a=3\) ta được phương trình \(y=3x+b\)
đường thẳng này cắt trục tung tại tung độ bằng 2
\(\Rightarrow\left(0;2\right)\)
\(\Rightarrow2=3.0+b\\ \Rightarrow b=2\)

\(a,PTHDGD:2x-1=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow M\left(1;1\right)\\ b,\text{Gọi đt của }\left(d\right)\text{ là }y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x+4\)

1) y= 2x-4
HD: y=ax+b
.... song song: a=2 và b≠-1
..... A(1;-2) => x=1 và y=-2 và Δ....
a+b=-2
Hay 2+b=-2 (thay a=2)
<=> b=-4
KL:................
2) Xét PT hoành độ giao điểm của (P) và (d)
x2=2(m-1)x-m+3 ⇔x2-2(m-1)x+m-3 =0 (1)
*) Δ'= (1-m)2-m+3= m2-3m+4=m2-2.\(\dfrac{3}{2}\)m+\(\dfrac{9}{4}\)+\(\dfrac{7}{4}\)=\(\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\). Vậy PT (1) có 2 nghiệm phân biệt x1; x2.
*) Theo hệ thức Viet ta có:
S=x1+x2=2(m-1) và P=x1.x2=m-3
*) Ta có: \(M=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
Thay S và P vào M ta có:
\(M=\left[2\left(m-1\right)\right]^2-2.\left(m-3\right)=4m^2-10m+10\\ =\left(2m\right)^2-2.2m.\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{15}{4}=\left(2m-\dfrac{5}{2}\right)^2+\dfrac{15}{4}\)
Vì (...)2≥0 nên M= (...)2+\(\dfrac{15}{4}\)≥\(\dfrac{15}{4}\)
Vậy M nhỏ nhất khi M=\(\dfrac{15}{4}\) khi 2m-\(\dfrac{5}{2}\)=0

Để tìm a và b, ta có các điều kiện sau:
Đường thẳng (d) có tung độ gốc là 1/3, tức là đường thẳng có dạng y = (1/3)x + b.Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 4, tức là khi x = 4, y = 0.Thay x = 4 và y = 0 vào phương trình đường thẳng, ta có:
0 = (1/3) * 4 + b 0 = 4/3 + b
Từ đó, ta có b = -4/3.
Vậy, phương trình đường thẳng (d) là: y = (1/3)x - 4/3.
(d) đi qua A(0;1/3) và B(4;0) nên ta có hệ phương trình:
0*a+b=1/3 và 4a+b=0
=>b=1/3 và 4a=-b=-1/3
=>a=-1/12 và b=1/3

a: Thay x=0 và y=0 vào \(\left(d\right)\), ta được:
k=0
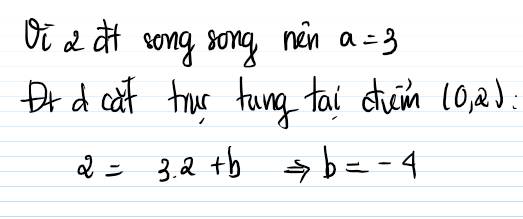
Gọi \(\left(d\right):y=ax+b\) là đt của (d)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne\sqrt{3}\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\Leftrightarrow2x-y+1=0\)
Khoảng cách từ K đến (d) là \(d\left(K;d\right)=\dfrac{6\cdot1-1+1}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)