Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
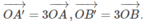
Vì O A → = ( 0 ; 4 ) nên O A ' → = ( 0 ; 12 ) . Do đó A′ = (0;12).
Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:
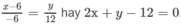
b) Có thể giải tương tự như câu a) .
Sau đây ta sẽ giải bằng cách khác.
Vì d 2 / / d nên phương trình của d 2 có dạng 2x + y + C = 0.
Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:
I A ' → = − 2 I A → hay x′ + 1 = −2, y′ − 2 = −4
Suy ra x′ = −3, y′ = −2
Do A' thuộc d 2 nên 2.(−3) – 2 + C = 0.
Từ đó suy ra C = 8
Phương trình của d 2 là 2x + y + 8 = 0

Phương trình đường thẳng d: 3x + y + 6 = 0
Lấy M(-2;0) thuộc d. Phép vị tự tâm O (0;0) tỉ số k = 2 biến d thành d’//d với d’ có dạng là 3x + y + c = 0 (c 6) và biến M thành M’ thì O M ' → = 2 O M →
⇔ x = 2. − 2 = − 4 y = 2.0 = 0 ⇒ M'(-4; 0)
Vì M thuộc d nên M’ thuộc d’, thay tọa độ M’ vào d’ ta được:
3.(-4) + 0 + c = 0 c = 12 (tm)
Phương trình đường thẳng d’: 3x + y + 12 = 0
Chọn đáp án D

Dễ thấy d chứa điểm \(H\left(1;1\right)\) và \(OH\perp d\). Gọi H' là ảnh của H qua phép quay tâm O góc \(45^0\) thì \(H=\left(0;\sqrt{2}\right)\)
Từ đó suy ra d' phải qua H' và vuông góc với O'. Vậy phương trình của d' là \(y=\sqrt{2}\)

Cách 1:
Lấy hai điểm A(0;2) và B (-1;-1) thuộc d. Gọi A' = (A), B' =
(B)
Khi đó A' = (0;2), B' = (1;-1). Vậy d' có phương trình =
hay 3x + y -2 =0
Cách 2:
Gọi M'(x', y') là ảnh của M (x;y) qua phép đối xứng trục Oy. Khi đó x' = -x và y' = y. Ta có M thuộc d ⇔ 3x-y+2 =0 ⇔ -3x' - y' + 2=0 ⇔ M' thuộc đường thẳng d' có phương trình 3x + y - 2 = 0
Cách 1:
Lấy hai điểm A(0;2) và B (-1;-1) thuộc d. Gọi A' = (A), B' =
(B)
Khi đó A' = (0;2), B' = (1;-1). Vậy d' có phương trình =
hay 3x + y -2 =0
Cách 2:
Gọi M'(x', y') là ảnh của M (x;y) qua phép đối xứng trục Oy. Khi đó x' = -x và y' = y. Ta có M thuộc d ⇔ 3x-y+2 =0 ⇔ -3x' - y' + 2=0 ⇔ M' thuộc đường thẳng d' có phương trình 3x + y - 2 = 0




Gọi \(M\left(x_0;y_0\right)\) là 1 điểm thuộc d \(\Rightarrow3x_0+y_0-2=0\) (1)
Gọi M' là ảnh của M qua phép vị tự tâm O tỉ số k \(\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=kx_M\\y_{M'}=ky_M\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_{M'}=-\frac{1}{2}x_0\\y_{M'}=-\frac{1}{2}y_0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=-2x_{M'}\\y_0=-2y_{M'}\end{matrix}\right.\)
Thế vào (1): \(3.\left(-2x_{M'}\right)-2y_{M'}-2=0\)
\(\Leftrightarrow3x_{M'}+y_{M'}+1=0\)
Vậy pt d' có dạng: \(3x+y+1=0\)