Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).

a) \(\overrightarrow{a}\left(2;3\right)\)
b) \(\overrightarrow{b}\left(5;-1\right)\)
c) \(\overrightarrow{m}\left(0;-4\right)\)

\(\left\{{}\begin{matrix}\overrightarrow{c}=\left(-m+5n;2m+n\right)\\\overrightarrow{v}=\left(9;4\right)\end{matrix}\right.\)
\(\overrightarrow{c}.\overrightarrow{v}=0\Leftrightarrow9\left(-m+5n\right)+4\left(2m+n\right)=0\)
\(\Leftrightarrow49n-m=0\Rightarrow m=49n\)
Mọi m;n thỏa mãn đẳng thức trên đều được

a) \(\overrightarrow{a}+\overrightarrow{b}=\left(2;-2\right)+\left(1;4\right)=\left(3;2\right)\).
\(\overrightarrow{a}-\overrightarrow{b}=\left(2;-2\right)-\left(1;4\right)=\left(1;-6\right)\).
\(2\overrightarrow{a}+3\overrightarrow{b}=2\left(2;-2\right)+3\left(1;4\right)=\left(4;-4\right)+\left(3;12\right)\)\(=\left(7;8\right)\).
c) Gọi x và y là hai số thực để:
\(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x\left(2;-2\right)+y\left(1;4\right)=\left(2x+y;-2x+4y\right)\)
Từ đó suy ra: \(\left\{{}\begin{matrix}2x+y=5\\-2x+4y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\).
Vậy \(\overrightarrow{c}=2\overrightarrow{a}+1\overrightarrow{b}\).

a) Đúng
b) Sai vì: \(\overrightarrow{a}+\overrightarrow{b}=\left(0;2\right)\ne\overrightarrow{0}\).
c) Sai vì \(\overrightarrow{a}+\overrightarrow{b}=\left(7;7\right)\ne\overrightarrow{0}\)
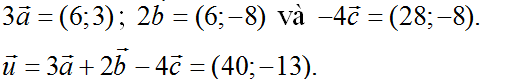
\(3\overrightarrow{a}=\left(0;3\right)\)
\(2\overrightarrow{b}=\left(-2;4\right)\)
\(-4\overrightarrow{c}\left(12;8\right)\)
=> \(\left\{\begin{matrix}u=0+3+12=15\\u=3+4+8=15\end{matrix}\right.\)
=>U(15;15)