Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Ảnh của A là:
x=1+3=4 và y=2+1=3
b: (d') là ảnh của (d) qua phép tịnh tiến vecto a=(3;-2)
=>(d'): x+y+c=0
Lấy B(1;4) thuộc (d)
=>B'(4;2)
Thay x=4 và y=2 vào (d'), ta được:
c+4+2=0
=>c=-6
d: Theo đề,ta có:
2+x=-1 và 4+y=3
=>x=-3 và y=-1
=>vecto u=(-3;-1)
Gọi G là điểm sao cho \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) (G là trọng tâm của tam giác ABC)
Khi đó \(G\left(2;4;3\right)\) và \(\overrightarrow{v}=\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}\)
Vậy điểm \(D\in\left(P\right)\) mà \(\left|\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right|\) bé nhất khi và chỉ khi D là hình chiếu của G trên mặt phẳng (P). Khi đó vecto \(\overrightarrow{GD}\) cùng phương với vecto pháp tuyến của (P) và điểm D nằm trên mặt phẳng (P) nên ta có hệ :
\(\begin{cases}\frac{x-2}{1}=\frac{y-4}{1}=\frac{z-3}{1}\\x+y+z-3=0\end{cases}\)
Giải hệ ta được : x = 0 ;y = 2; z = 1
Vậy điểm D cần tìm là \(D\left(0;2;1\right)\)
Chọn B
Δ có vectơ chỉ phương 
và đi qua A (1;1;-2) nên có phương trình:
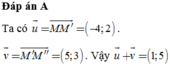
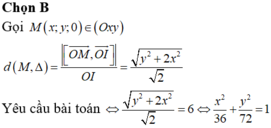
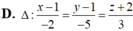
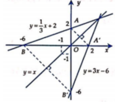
Ý bạn là phương trình đường thẳng?
Gọi \(M\left(x;y\right)\) là điểm thuộc \(\Delta\) và \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow\left\{{}\begin{matrix}x'=x-3\\y'=y+2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'+3\\y=y'-2\end{matrix}\right.\)
\(\Rightarrow\left(x'+3\right)-3\left(y'-2\right)+6=0\)
\(\Leftrightarrow x'-3y'+15=0\)
Vậy phương trình \(\Delta':\) \(x-3y+15=0\)