Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T=\dfrac{1}{f}=10^{-6}s\)
Năng lượng từ trường trong mạch có giá trị bằng nửa giá trị cực đại của nó sau những khoảng thời gian:
\(t=\dfrac{T}{4}=0,25\mu s\)
=> Ko có đáp án nào đúng

Đáp án D.

Tại thời điểm t = 0
w d = w d m a x ⇒ q 2 0 2 C = Q 2 0 2 C ⇒ q 0 = ± Q 0
khi w d = 1 2 w d m a x ⇒ q 2 2 C = 1 2 . Q 2 0 2 C ⇒ q = ± Q 0 2
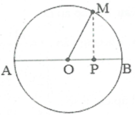
Thời gian ngắn nhất là thời gian biến thiên từ Q 0 đến Q 0 / 2 , tương ứng với thời gian chuyển động từ B đến P (hình vẽ dưới đây), trong đó: OP = OB/ 2
Dễ thấy:
C o s M O P = O P O M = 1 2 ⇒ M O P = π 4 t = 45 0 360 0 T = 1 8 . 1 10 6 = 0 , 125 . 10 - 6 s

Đáp án D.
Tại thời điểm t = 0
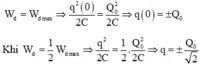
Thời gian ngắn nhất là thời gian biến thiên từ Q 0 đến Q 0 2 , tương ứng với thời gian chuyển động từ B đến P (hình vẽ dưới đây), trong đó: O P = O B 2
Dễ thấy:
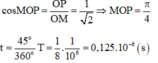

Chọn đáp án C
Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là, tức là
Δ t : Q 0 2 2 C → 1 2 Q 0 2 2 C ⇔ q = Q 0 → q = Q 0 2 ⇒ Δ t = T 8 ⇔ T = 8 Δ t
Thời gian ngắn nhất để điện tích trên tụ có độ lớn giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại, tức là
Δ t ' : q = Q 0 → q = Q 0 2 ⇒ Δ t ' = T 6 = 8 Δ t 6 = 4 Δ t 3

Chọn đáp án C
Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là, tức là
Δ t : Q 0 2 2 C → 1 2 Q 0 2 2 C ⇔ q = Q 0 → q = Q 0 2 ⇒ Δ t = T 8 ⇔ T = 8 Δ t
Thời gian ngắn nhất để điện tích trên tụ có độ lớn giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại, tức là
Δ t ' : q = Q 0 → q = Q 0 2 ⇒ Δ t ' = T 6 = 8 Δ t 6 = 4 Δ t 3

Hướng dẫn: Chọn đáp án A
Thời gian ngắn nhất để năng lượng điện trường giảm từ giá trị cực đại (giả sử lúc này q = Q 0 ) xuống còn một nửa giá trị cực đại ( q = Q 0 2 ) là T 8 = 1 , 5.10 − 4 s, suy ra T = 1 , 2.10 − 3 s
Thời gian ngắn nhất để điện tích trên tụ giảm từ giá trị cực đại xuống còn một nửa giá trị đó là T 6 = 2.10 − 4 s
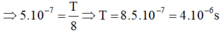
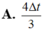
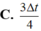



\(T = 1/f = 0,001s.\)
\(W_L = \frac{1}{2}W_{Lmax}=> \frac{1}{2}Li^2= \frac{1}{2}\frac{1}{2}LI_0^2.\)
=> \(i= \pm \frac{I_0}{\sqrt{2}}.\)
Thời gian để năng lượng từ trường lại bằng một nửa giá trị cực đại của nó là
I 0 -I 0 I 0 -I 0 2 2
\(\cos \varphi_1 = \frac{I_0/\sqrt{2}}{I_0}= \frac{1}{\sqrt{2}}=> \varphi _1= \frac{\pi}{4}=> \varphi = \frac{\pi}{2}.\)
\(t = \frac{\varphi}{\omega}= \frac{\pi/2}{2\pi/T}= \frac{T}{8}=2,5.10^{-4}s.\)