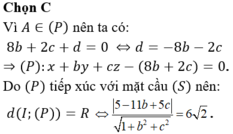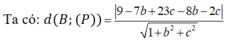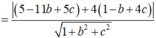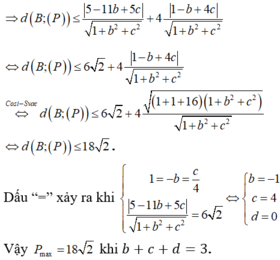Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt cầu (S) tâm O bán kính R=3
Gọi I là hình chiếu vuông góc của O lên (P)
Phương trình đường thẳng d qua O và vuông góc (P) có dạng: \(\left\{{}\begin{matrix}x=2t\\y=t\\z=2t\end{matrix}\right.\)
Tọa độ I thỏa mãn: \(8t+2t+8t+7=0\Rightarrow t=-\frac{7}{18}\Rightarrow I\left(-\frac{7}{9};-\frac{7}{18};-\frac{7}{9}\right)\)
Gọi \(r\) là bán kính đường tròn giao tuyến (S) và (P), ta có \(OI=\frac{7}{6}\Rightarrow r=\frac{5\sqrt{11}}{6}\)
Mặt cầu chứa đường tròn giao tuyến trên có tâm nằm trên d nên gọi tọa độ tâm có dạng \(A\left(2a;a;2a\right)\) và bán kính \(R'\)
\(\left\{{}\begin{matrix}R'=d\left(A;\left(Q\right)\right)\\R'=\sqrt{d^2\left(A;\left(P\right)\right)+r^2}\end{matrix}\right.\)
\(\Rightarrow\frac{\left|3a-8a-20\right|}{\sqrt{3^2+\left(-4\right)^2}}=\sqrt{\frac{\left(8a+2a+8a+7\right)^2}{4^2+2^2+4^2}+\frac{275}{36}}\)
\(\Leftrightarrow\frac{\left(5a+20\right)^2}{25}=\frac{\left(18a+7\right)^2+275}{36}\)
\(\Leftrightarrow8a^2-a-7=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-\frac{7}{8}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}R_1=5\\R_2=\frac{25}{8}\end{matrix}\right.\)

Phương trình đường thẳng d qua A và vuông góc \(\left(\alpha\right)\): \(\left\{{}\begin{matrix}x=t\\y=1-t\\z=2+t\end{matrix}\right.\)
Giao điểm B của d và \(\left(\alpha\right)\): \(t-\left(1-t\right)+2+t-4=0\Rightarrow t=1\Rightarrow B\left(1;0;3\right)\)
Gọi phương trình (P): \(ax+by+cz+d=0\)
Do (P) chứa A và B \(\Rightarrow\left\{{}\begin{matrix}b+2c+d=0\\a+3c+d=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=-a-3c\\b=a+c\end{matrix}\right.\)
\(\Rightarrow ax+\left(a+c\right)y+cz-a-3c=0\)
\(d\left(I;\left(P\right)\right)=\frac{\left|3a+a+c+2c-a-3c\right|}{\sqrt{a^2+\left(a+c\right)^2+c^2}}=\frac{\left|3a\right|}{\sqrt{2a^2+2c^2+2ac}}=k\ge0\)
Để bán kính đường tròn là nhỏ nhất \(\Rightarrow k\) lớn nhất
- Với \(c=0\Rightarrow k=\frac{3}{\sqrt{2}}\)
- Với \(c\ne0\):
\(\left|3a\right|=k\sqrt{2a^2+2ac+2c^2}\Leftrightarrow\left(2k^2-9\right)a^2+2k^2c.a+2k^2c^2=0\)
\(\Delta'=\left(k^2c\right)^2-2k^2c^2\left(2k^2-9\right)=-3k^4c^2+18k^2c^2\)
\(\Delta'\ge0\Rightarrow3k^2c^2\left(6-k^2\right)\ge0\Rightarrow k^2\le6\Rightarrow k\le\sqrt{6}\)
So sánh 2 giá trị \(k=\sqrt{6}\) và \(k=\frac{3}{\sqrt{2}}\Rightarrow k_{max}=\sqrt{6}\)
Khi đó \(a=\frac{-2k^2c}{2\left(2k^2-9\right)}=-2c\)
\(\Rightarrow\left(P\right):\) \(-2cx-cy+cz-c=0\Leftrightarrow2x+y-z+1=0\)
\(\Rightarrow M\left(-\frac{1}{2};0;0\right)\)