Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên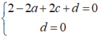 
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
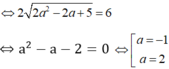
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó 
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0
6.
Mặt cầu bán kính \(R=2\)
Thể tích: \(V=\frac{4}{3}\pi R^3=\frac{32\pi}{3}\)
7.
Chắc bạn ghi nhầm, pt có lý là: \(x^2+y^2+z^2-8x+10y-6z+49=0\)
Tọa độ tâm \(I\left(4;-5;3\right)\)
Bán kính: \(R=\sqrt{4^2+5^2+3^2-49}=1\)
8.
Phương trình mặt phẳng:
\(2\left(x-1\right)+3\left(y-2\right)+5\left(z-4\right)=0\)
\(\Leftrightarrow2x+3y+5z-28=0\)
1.
\(\overrightarrow{AB}=\left(-7;5;0\right)\) ; \(\overrightarrow{AC}=\left(-5;4;3\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(15;21;-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=\sqrt{15^2+21^2+3^2}=\frac{15\sqrt{3}}{2}\)
2.
\(\overrightarrow{u}.\overrightarrow{v}=1.0+0.1+2.\left(-2\right)=-4\)
3.
Gọi \(M\left(0;m;0\right)\) là điểm thuộc trục tung
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+3;7\right)\\\overrightarrow{BM}=\left(-5;m-7;5\right)\end{matrix}\right.\)
\(AM=BM\Leftrightarrow1^2+\left(m+3\right)^2+7^2=5^2+\left(m-7\right)^2+5^2\)
\(\Leftrightarrow6m+59=-14m+99\Rightarrow m=2\Rightarrow M\left(0;2;0\right)\)
4.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|2-3-1+5\right|}{\sqrt{2^2+3^2+1^2}}=\frac{3}{\sqrt{14}}\)
Phương trình đường tròn: \(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+1\right)^2=\frac{9}{14}\)
5.
\(\overrightarrow{IA}=\left(3;-2;4\right)\Rightarrow R=IA=\sqrt{3^2+2^2+4^2}=\sqrt{29}\)
Pt mặt cầu: \(\left(x-2\right)^2+\left(y-4\right)^2+\left(z+1\right)^2=29\)
