Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

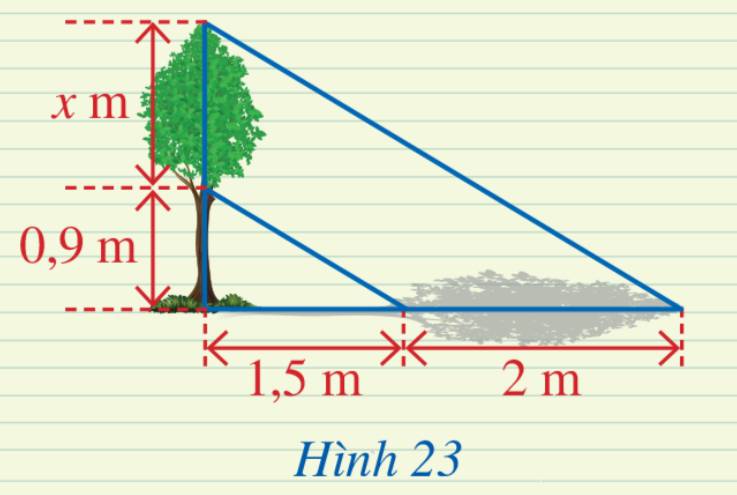
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AD và DB biểu thị độ cao của thân và tán cây, đoạn thẳng AE và EC biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng DE và BC biểu thị cho các tia nắng.
Xét tam giác ABC với \(DE\parallel BC\) ta có:
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) (Định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{0,9}}{x} = \frac{{1,5}}{2}\\ \Rightarrow 0,9.2 = 1,5x\\ \Rightarrow 1,8 = 1,5x\\ \Rightarrow x = 1,2\end{array}\)
Vậy độ cao \(x\) là 1,2 m.

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)

Vì tổng ba góc trong một tam giác bằng \(180^\circ \) nên nếu \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) thì \(\widehat {MPN} = \widehat {CBA}\)
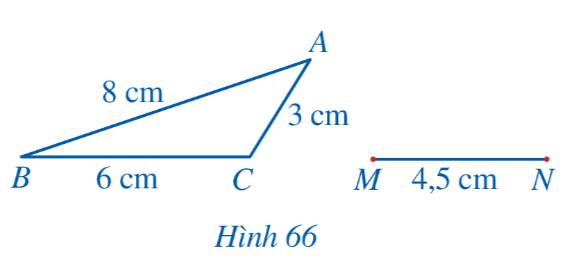
Ta cần \(\Delta ABC \backsim\Delta NPM\)
Khi đó \(\frac{{AB}}{{NP}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{NM}}\) hay \(\frac{8}{{NP}} = \frac{6}{{PM}} = \frac{3}{{4,5}} = \frac{2}{3}\)
Ta có: \(\frac{8}{{NP}} = \frac{2}{3} \Rightarrow NP = 8.3:2 = 12cm\)
\(\frac{6}{{MP}} = \frac{2}{3} \Rightarrow MP = 6.3:2 = 9cm\)
Vậy Thanh cần dùng thước kẻ vẽ hai đoạn thẳng NP=12cm và PM=9cm để tìm được điểm P thỏa mãn yêu cầu đề bài.

Nhìn vào biểu đồ, tương ứng với các mốc thời gian, số ở cột màu xanh biểu diễn GDP của Việt Nam và số ở cột màu đổ biểu diễn GDP của Singapore.
Ta xác định được GDP của hai nước trong các năm 2016, 2017, 2018 như sau:
Việt Nam:
Năm 2016: 205,3 tỉ đô la Mỹ
Năm 2017: 223,7 tỉ đô la Mỹ
Năm 2018: 245,2 tỉ đô la Mỹ
Singapore:
Năm 2016: 318,7 tỉ đô la Mỹ
Năm 2017: 341,9 tỉ đô la Mỹ
Năm 2018: 373,2 tỉ đô la Mỹ

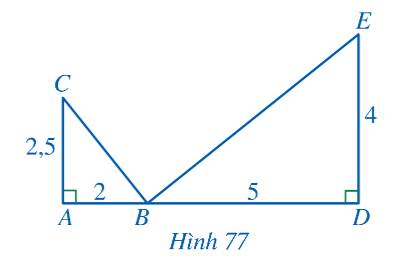
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).

\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow B'C' = \frac{{BC.A'B'}}{{AB}}\).

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

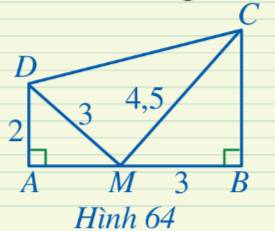
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).

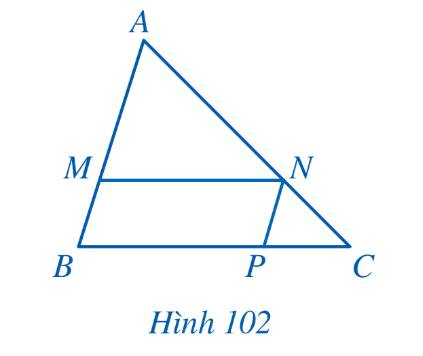
Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (Định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)




Từ bài tập 2 trang 57 Sách giáo khoa Toán 8 – Cánh diều ta có kết quả: Đường thẳng song song với hai đáy của hình thang thì định ra trên hai cạnh bên các đoạn thẳng tỉ lệ.
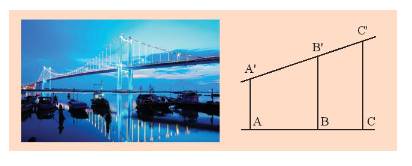
Do các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau nên ta có các hình thang ACC’A’, BDD’B’.
Xét hình thang ACC’A’ với BB’ song song với hai đáy AA’ và CC’, ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\,\,\left( 1 \right)\)
Xét hình thang BDD’B’ với CC’ song song với hai đáy BB’ và DD’, ta có:
\(\frac{{BC}}{{CD}} = \frac{{B'C'}}{{C'D'}} \Rightarrow \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\)
Vậy độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A’B’, B’C’, C’D’.