Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

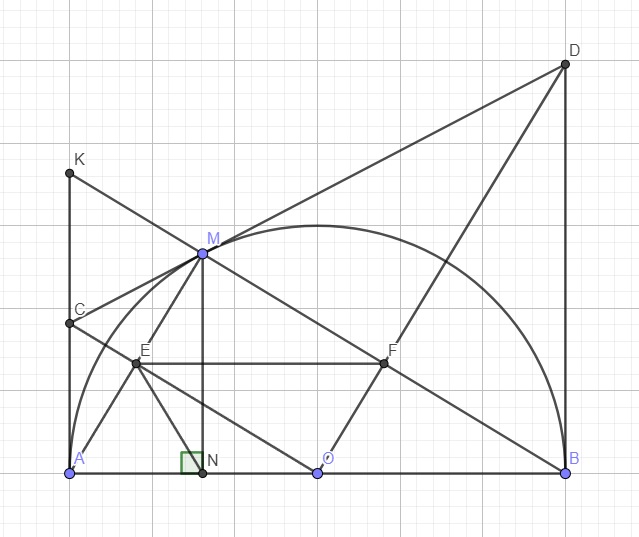
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân

a: góc BEA=1/2*180=90 độ
góc KEF+góc KMF=180 độ
=>KEFM nội tiếp
b: góc FAB=góc FAM+góc BAM
=1/2*góc IAM+góc BAM
=1/2*(1/2*sđ cung AM+sđ cung MB)
=1/2(1/2*sđ cung AM+180 độ-sđ cung AM)
=1/2(180 độ-1/2*sđ cung AM)
=90 độ-góc FAM
góc BFA=90 độ-góc FAM
=>góc BAF=góc BFA
=>ΔBAF cân tại B

a: góc BEA=1/2*180=90 độ
góc KEF+góc KMF=180 độ
=>KEFM nội tiếp
b: góc FAB=góc FAM+góc BAM
=1/2*góc IAM+góc BAM
=1/2*(1/2*sđ cung AM+sđ cung MB)
=1/2(1/2*sđ cung AM+180 độ-sđ cung AM)
=1/2(180 độ-1/2*sđ cung AM)
=90 độ-góc FAM
góc BFA=90 độ-góc FAM
=>góc BAF=góc BFA
=>ΔBAF cân tại B

1: Vì A,E,M,B cùng nằm trên (O)
nên AEMB nội tiếp
góc AMB=1/2*180=90 độ
=>AM vuông góc IB
ΔIAB vuông tại A có AM vuông góc IB
nên IA^2=IM*IB