Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O M
a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)

a: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
=>ΔABC đòng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
b: góc AMO=góc ABO=90 độ
=>ABMO nội tiếp, I là trung điểm của AO

a: AB=8cm
=>BM=4cm
b: Xét ΔMAC và ΔMBD có
MA=MB
góc AMC=góc BMD
MC=MD
Do đo: ΔMAC=ΔMBD
Suy ra: AC=BD
c: AC+BC=BD+BC>CD=2CM

a: OB=10-3=7cm
=>OB>BM
=>M nằm giữa O và B
b: OM=AM-AO=2cm

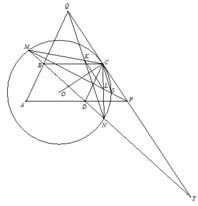
1). Gọi MN giao PQ tại T. Theo định lí Thales, ta có T P T C = T D T B = T C T Q .
Từ đó T C 2 = T P . T Q .
Do TC là tiếp tuyến của (O), nên T C 2 = T M . T N .
Từ đó T M . T N = T C 2 = T P . T Q , suy ra tứ giác MNPQ nội tiếp.
a: AC=AB-BC=5-2=3cm
BD=AD-AB=3cm
=>AC=BD
b: CD=AD-AC=8-3=5cm
AB=AD-BD=8-3=5cm
=>CD=AB