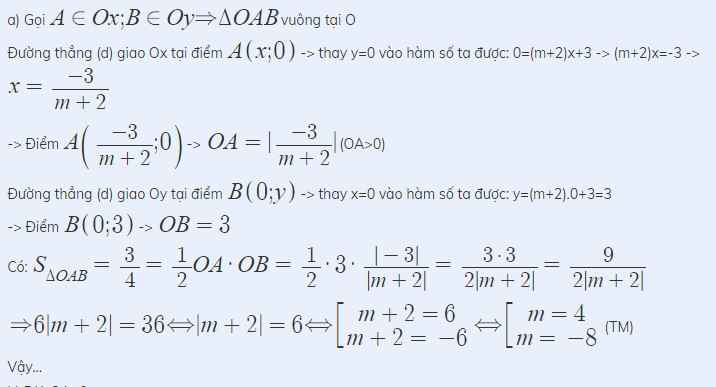Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý :
a) y = 2 => x = 2 hoặc -2 ( do có thể < 0 hay > 0 )
b) S(OAB) = 1 => |x| = 1 => x = 1 hoặc -1
c) Gọi khoảng cách từ O tới (d) là OH
OH bé hơn hoặc bằng khoảng cách 2 của O tới điểm cố định trên Oy
=> max = 2 khi d song^2 Ox => x = 0 => đúng mọi m
d) Thay vào biểu thức hệ thức lượng => khoảng cách từ O tới điểm mà d cắt trên Ox là 0 => d trùng Oy
e) thay x vào có kết quả
f) cắt tại điểm > 2 => biểu thức biểu diễn x > 2 ( -2/(m+3) )

a) Gọi \(A\in Ox;B\in Oy\Rightarrow\Delta OAB\)vuông tại O
Đường thẳng (d) giao Ox tại điểm \(A\left(x;0\right)\)-> thay y=0 vào hàm số ta được: 0=(m+2)x+3 -> (m+2)x=-3 -> \(x=\frac{-3}{m+2}\)
-> Điểm \(A\left(\frac{-3}{m+2};0\right)\)-> \(OA=|\frac{-3}{m+2}|\)(OA>0)
Đường thẳng (d) giao Oy tại điểm \(B\left(0;y\right)\)-> thay x=0 vào hàm số ta được: y=(m+2).0+3=3
-> Điểm \(B\left(0;3\right)\)-> \(OB=3\)
Có: \(S_{\Delta OAB}=\frac{3}{4}=\frac{1}{2}OA\cdot OB=\frac{1}{2}\cdot3\cdot\frac{|-3|}{|m+2|}=\frac{3\cdot3}{2|m+2|}=\frac{9}{2|m+2|}\)
\(\Rightarrow6|m+2|=36\Leftrightarrow|m+2|=6\Leftrightarrow\orbr{\begin{cases}m+2=6\\m+2=-6\end{cases}}\Leftrightarrow\orbr{\begin{cases}m=4\\m=-8\end{cases}}\)(TM)
Vậy...
b) ĐK: OA>0
\(\Delta OAB\)vuông tại O -> \(AB=\sqrt{OA^2+OB^2}=\sqrt{3^2+\left(\frac{-3}{m+2}\right)^2}=\sqrt{9+\frac{9}{\left(m+2\right)^2}}\)
Kẻ \(OH\perp d\)tại H -> OH là khoảng cách từ đường thẳng từ O đến d
Áp dụng htl trong \(\Delta OAB\)vuông tại O, đường cao OH -> \(OA.OB=OH.AB\)
\(\rightarrow3\cdot\frac{|-3|}{|m+2|}=\frac{3\sqrt{2}}{2}.\sqrt{9+\frac{9}{\left(m+2\right)^2}}\)
\(\Leftrightarrow\left(3\cdot\frac{|-3|}{|m+2|}\right)^2=\left(\frac{3\sqrt{2}}{2}\right)^2\left(9+\frac{9}{\left(m+2\right)^2}\right)\)
\(\Leftrightarrow\frac{81}{\left(m+2\right)^2}=\frac{9\cdot9}{2}+\frac{9\cdot9}{2\left(m+2\right)^2}\Leftrightarrow\frac{81}{\left(m+2\right)^2}=\frac{81}{2}+\frac{81}{2\left(m+2\right)^2}\)
\(\Leftrightarrow\frac{1}{\left(m+2\right)^2}-\frac{1}{2}-\frac{1}{2\left(m+2\right)^2}=0\Leftrightarrow\frac{2-\left(m+2\right)^2-1}{2\left(m+2\right)^2}=0\) ( \(2\left(m+2\right)^2>0\))
\(\Rightarrow1-\left(m+2\right)^2=0\Rightarrow\left(m+2\right)^2=1\Leftrightarrow\orbr{\begin{cases}m+2=1\\m+2=-1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m=-1\\m=-3\end{cases}}\)(TM)
Vậy...
Hì cậu kiểm tra xem tớ có sai dấu hay sai bước chỗ nào với nhé vì tớ hay cẩu thả lắm:'33

a: Tọa độ A là:
y=0 và mx-2m-1=0
=>\(\left\{{}\begin{matrix}x=\dfrac{2m+1}{m}\\y=0\end{matrix}\right.\)
Tọa độ B là:
x=0 và y=m*0-2m-1=-2m-1
b: A(2m+1/m;0); O(0;0); B(0;-2m-1)
=>OA=|2m+1|/|m|;OB=|2m+1|
Theo đề, ta có: \(\dfrac{1}{2}\cdot OA\cdot OB=2\)
=>(2m+1)^2/|m|=4
TH1: m>0
=>4m^2+4m+1=4m
=>4m^2+1=0(loại)
TH2: m<0
=>4m^2+4m+1=-4m
=>4m^2+8m+1=0
=>\(\left[{}\begin{matrix}m=\dfrac{-2+\sqrt{3}}{2}\\m=\dfrac{-2-\sqrt{3}}{2}\end{matrix}\right.\)
c: \(h\left(O;d\right)=\dfrac{\left|0\cdot m+0\cdot\left(-1\right)-2m-1\right|}{\sqrt{m^2+1}}=\dfrac{\left|2m+1\right|}{\sqrt{m^2+1}}\)