Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn lưu ý, là bài này khác bài kia là A sớm pha hơn B nhé.
Do A sớm pha hơn B là \(\frac{\pi}{2}\) nên tương tự bài trước, mình lấy điểm A' cùng pha với B.
Do đó, A'A = \(\frac{\lambda}{4}\)
Điểm M dao động biên độ cực tiểu khi: \(d_2-\left(d_1-\frac{\lambda}{4}\right)=\left(k+\frac{1}{2}\right)\lambda\Rightarrow d_2-d_1=\left(k+\frac{1}{4}\right)\lambda\)
Theo đáp án, ta có: \(d_2-d_1=-1,75cm=\left(-2+\frac{1}{4}\right)\lambda\)
Nên M dao động cực tiểu.

Điểm M dao động với biên độ cực đại thì: \(MA-\left(MB-\frac{\Delta\varphi}{2\pi}\lambda\right)=k\lambda\)
\(\Rightarrow MA-MB=k\lambda-\frac{\Delta\varphi}{2\pi}\lambda\)
Thay \(\Delta\varphi=-\frac{\pi}{3}\) vào biểu thức trên thì: \(\Rightarrow MA-MB=k\lambda-\frac{\lambda}{6}=\frac{\lambda}{3}\)(giả thiết)
Không tìm đc giá trị nguyên k thỏa mãn PT trên, nên \(\Delta\varphi=-\frac{\pi}{3}\) không thỏa mãn.
bạn ơi đấy là đáp án D trong ABCD
A. -pi/6 b. -2pi/3 c.2pi/3 d. -pi/3
cả A và B đều không thỏa mãn giống D mà

Giữa M và trung trực của AB có 2 cực đại khác nên M là cực đại thứ 3 kể từ trung trực.
Vì: \(d_1-d_2=\text{k}\lambda-\frac{\lambda}{6}\)
Nên: k = 1 là cực đại thứ 1 (để cho d1 - d2 > 0).
k = 2 là cực đại thứ 2.
M là cực đại thứ 3 nên k = 3 bạn nhé.

Đáp án C
+ Biên độ sóng tổng hợp A M = 2 acos ( π d 1 - d 2 λ )

Chọn đáp án D
λ = v f = 60 c m u = 2 A cos π ( d 1 - d 2 ) λ cos 10 π t - π ( d 1 - d 2 ) λ = 4 cos π 12 cos 10 π t - 7 π 12

Đáp án D
+ Với hai nguồn cùng pha, khi xảy ra giao thoa thì trung trực của AB là một cực đại ứng với k = 0 là cực đại, giữa M và trung trực có 1 dãy cực đại nữa thì M là cực đại ứng với k = 2
+ Ta có d 2 - d 1 = n v f ⇒ v = ( d 2 - d 1 ) f n = ( 26 , 2 - 23 ) . 15 2 = 24 cm / s .

Chọn A
+ M là một cực đại giao thoa, giữa M và trung trực còn một đường không dao động Suy ra M là cực đại ứng với k = 1.
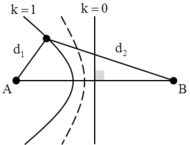
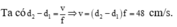


M thuộc đường cực đại gần trung trực của AB nhất => M thuộc giao của hypebol cực đại với đoạn AB.
\(d_{AM}=\frac{AB}{2}+\frac{\lambda}{6}.\)
\(d_{BM}=\frac{AB}{2}-\frac{\lambda}{6}.\)
=> \(d_{AM}-d_{BM}=\frac{\lambda}{3}.\)
Mà M là cực đại nên vị trí của nó cách hai nguồn phải thỏa mãn
\(d_2-d_1=\left(k+\frac{\Delta\varphi}{2\pi}\right)\lambda.\)
=> \(\left(k+\frac{\Delta\varphi}{2\pi}\right)\lambda=\frac{\lambda}{3}\)
=> \(\left(k+\frac{\Delta\varphi}{2\pi}\right)=\frac{1}{3}\)
Mà M gần nhất => k = 0 => \(\Delta\varphi=\frac{2\pi}{3}.\)
A B M d1 d2 B'
Mình giải thích chi tiết hơn công thức của bạn Giang Nam thế này:
B sớm pha hơn A là \(\frac{\pi}{3}\)
Mình lấy điểm B' trên phương truyền sóng BM sao cho B' cùng pha với A, nên B' trễ pha \(\frac{\pi}{3}\)so với B \(\Rightarrow BB'=\frac{\lambda}{6}\)
B' cùng pha với A nên B dao động cực đại thì: \(MB'-MA=k\lambda\Leftrightarrow\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\)
\(\Leftrightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)(Trong công thức của bạn Giang Nam phải sửa lại như thế này mới đúng đc)
Dựa theo các phương án của bài toán thì d1=12cm, d2 = 18cm thỏa mãn công thức trên nên điểm M dao động biên cực đại.
Điểm M dao động với biên cực đại khi: \(d_2-\left(d_1-\frac{\lambda}{6}\right)=k\lambda\Rightarrow d_2-d_1=k\lambda-\frac{\lambda}{6}\)
Thử giá trị: \(d_2-d_1=6,5=2\lambda-\frac{\lambda}{6}\) thỏa mãn điều kiện cực đại ở trên nên điểm M dao động với biên cực đại.