Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

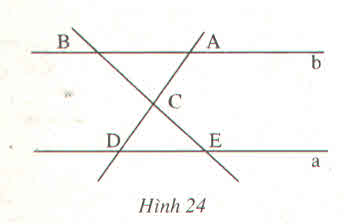
Ta có:
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.


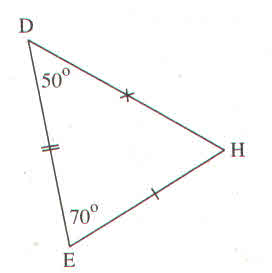
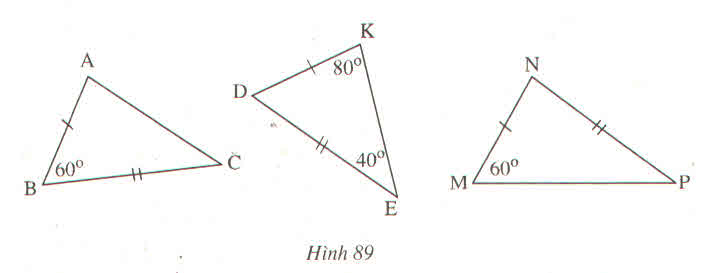
Tam giác DKE có:
\(\widehat{D}+\widehat{K}+\widehat{E}\)=1800 (tổng ba góc trong của tam giác).
\(\widehat{D}\)+800 +400=1800
\(\widehat{D}\)=1800 -1200= \(60^0\)
Nên ∆ ABC và ∆KDE có:
AB=KD(gt)
\(\widehat{B}\)=\(\widehat{D}\)=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại.

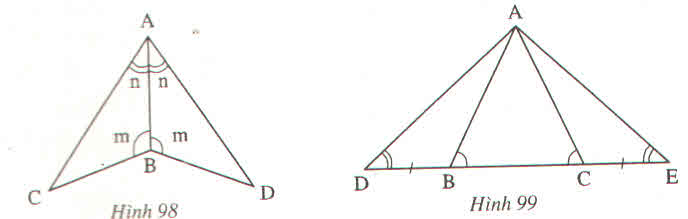
- Xem hình 98
∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
- Xem hình 99.
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)





D
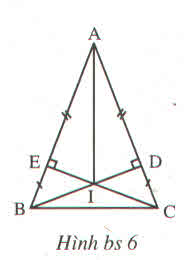
Xét tam giác AIE và tam giác AID có:
AE = AD (theo đề bài)
góc AEI = góc ADI = \(90^0\)
AI là cạng chung
Do đó tam giác AIE = tam giác AID (cạnh huyền và cạnh góc vuông) úuy ra góc A1 = A2 (2 góc tương ứng) (1)
Suy ra: EI = DI (2 cạnh tương ứng)(*)
Xét tam giác IEB và tam giác IDC có:
EI = DI (*)
góc IEB = góc IDC = \(90^0\)
EB = DC ( theo đề bài)
Do đó tam giác IEB = tam giác IDC (2 cạnh góc vuông)
Có BE + AE = AB
CD + AD = AC
mà: AE = AD, EB = DC (theo đề bài)
Suy ra: AB = AC (2)
Xét tam giác AIB và tam giác AIC có:
AB = AC (2)
góc A1 = góc A2 (1)
AI là cạnh chung
Do đó: tam giác AIB = tam giác AIC (c.g.c)
Xét tam giác ECB và tam giác DBC có:
EB = DC ( theo đề bài)
góc CEB = góc BDC = \(90^0\)
Do đó: tam giác ECB = tam giác DBC (cạnh huyền và cạnh góc vuông)
Suy ra: EC = BD (2 cạnh tương ứng) (3)
Xét tam giác AEC và tam giác ADB có:
AE = AD (theo đề bài)
góc AEC = góc ADB = \(90^0\)
EC = BD (3)
Do đó: tam giác AEC = tam giác ADB ( 2 cạnh góc vuông)
Vậy đáp án đúng là: (D) 5 cặp tam giác bằng nhau trong hình bs 6