
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A=2+2^2+2^3+2^4+2^5+2^6+2^7+2^8+2^9+2^10
=(2+2^2)+(2^3+2^4)+(2^5+2^6)+(2^7+2^8)+(2^9+2^10)
=2(1+2)+2^3(1+2)+2^5(1+2)+2^7(1+2)+2^9(1+2)
=(1+2)(2+2^3+2^5+2^7+2^9)
=3(2+2^3+2^5+2^7+2^9) chia hết cho 3

\(=2\left(1+2\right)+2^3\left(1+2\right)+2^5\left(1+2\right)+2^7\left(1+2\right)+2^9\left(1+2\right)\)
\(=3\left(2+2^3+2^5+2^7+2^9\right)⋮3\)

Ta có :
\(2+2^2+2^3+....+2^{10}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+....+2^9\left(1+2\right)\)
\(=2.3+2^3.3+....+2^9.3\)
=> Tổng chia hết cho 3
\(2+2^2+2^3+...+2^{10}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^9+2^{10}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^9\left(1+2\right)\)
\(=2.3+2^3.3+...+2^9.3\)
\(=\left(2+2^3+...+2^9\right).3⋮3\)
\(\Rightarrow2+2^2+2^3+...+2^{10}⋮3\)
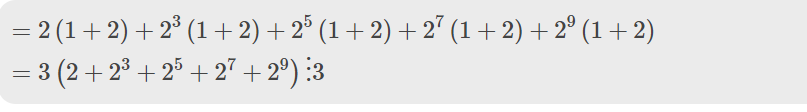
Có nha bạn.
Có nha bạn.