B
7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 5 2021
...............................................................................................................................................................................................................................................? chịu thua
DH
0
NV
0
NB
1
HN
13 tháng 6 2021
Các số nghịch đảo:
\(2\rightarrow\frac{1}{2};6\rightarrow\frac{1}{6};12\rightarrow\frac{1}{12};...;90\rightarrow\frac{1}{90}\)
Gọi A là tổng các số nghịch đảo
\(A=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{90}\\ =\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{9\cdot10}\\ =1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\\ =1-\frac{1}{10}=\frac{9}{10}\)
BV
1
SG
3
HT
15 tháng 5 2017
\(\dfrac{1}{-2}=-\dfrac{1}{2}=-\dfrac{6}{12}=\dfrac{\left(-3\right)+\left(-2\right)+\left(-1\right)}{12}=-\dfrac{1}{4}+-\dfrac{1}{6}+-\dfrac{1}{12}=\dfrac{1}{-4}+\dfrac{1}{-6}+\dfrac{1}{-12}\)\(\rightarrow\) \(-2\) đã đượcviết dưới dạng tổng 3 số nghịch đảo của 3 số nguyên \(-4,-6,-12\)
12 tháng 4 2018
Số nghịch đảo của -2 là (-1)/2
Ta có: 
Nghịch đảo của ba số: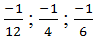 
là lượt là: -12, -4, -6
Vậy số nghịch đảo của -2 được viết dưới dạng tổng nghịch đảo của ba số nguyên là -4; -6; -12.
DT
4
YA
1
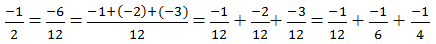
Tổng các nghịch đảo của các số sau : 120 , 168 , 224 , 288 ,..........., 9800 là:
\(\frac{1}{120}+\frac{1}{168}+\frac{1}{224}+.....+\frac{1}{9800}\)
=\(\frac{1}{10.12}+\frac{1}{12.14}+\frac{1}{14.16}+......+\frac{1}{98.100}\)
=\(\frac{1.2}{10.12.2}+\frac{1.2}{12.14.2}+\frac{1.2}{14.16.2}+......+\frac{1.2}{98.100.2}\)
=\(\frac{1}{2}.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{98}-\frac{1}{100}\right)\)
=\(\frac{1}{2}.\left(1-\frac{1}{100}\right)=\frac{1}{2}.\frac{99}{100}=\frac{99}{200}\)
Tổng nghịch đảo của các số đó là
A=\(\frac{1}{120}+\frac{1}{168}+\frac{1}{224}+...+\frac{1}{9800}\)
\(4A=\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+...\frac{1}{2450}\)
\(4A=\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{49}-\frac{1}{50}\)
\(4A=\frac{1}{5}-\frac{1}{50}=\frac{9}{50}\)
A=9/200
Tổng nghịch đảo của chúng là 9/200