
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

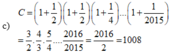

C = 1+1/2(1+2)+1/3(1+2+3)+........+1/2015(1+2+3+4+...+2015)
C = 1 + \(\frac{1}{2}\cdot\frac{2.3}{2}\)+ \(\frac{1}{3}\cdot\frac{3.4}{2}\)+ ... + \(\frac{1}{2015}\cdot\frac{2015.2016}{2}\)
C = \(\frac{2}{2}\) + \(\frac{3}{2}+\frac{4}{2}+...+\frac{2016}{2}\)
C = \(\frac{2+3+4+...+2016}{2}\)
Đặt D = 2 + 3 + 4 + ... + 2016
Số số hạng của D là : (2016 - 2) : 1 + 1 = 2015
Tổng D là : (2 + 2016) . 2015 : 2 = 2033135
Thay D vào biểu thức C ta được : \(\frac{2033135}{2}\)
Vậy C = ... .

a/A=1+2+4+8+...+1024
2A=2+4+8+16+....+2048
2A-A=(2+4+8+16+....+2048)-(1+2+4+8+...+1024)
A=2048-1
A=2047
VẬY A=2047
b/B=1+5+25+125+....+15625
5B=5+25+125+625+....+78125
5B-B=(5+25+125+625+....+78125)-(1+5+25+125+....+15625)
4B=78125-1
4B=78124
B=78124:4
B=19531
VẬY B =19531
C=1/1.2+1/2.3+1/3.4+...+1/2015.2016
C=1-1/2+1/2-1/3+1/3-1/4+...+1/2015-1/2016
=1-1/2016
=2015/2016
VẬY C=2015/2016
D/=10/1.3+10/3.5+10/5.7+....+10/2013.2015
=5(2/1.3+2/3.5+2/5.7+...+2/2013.2015)
=5(1-1/3+1/3-1/5+1/5-1/7+..+1/2013-1/2015)
=5(1-1/2015)
=5.2014/2015
=2014/403
VẬY D=2014/403
a, A = 1 + 2 + 4 + 8 +...+ 1024
\(A=1+2+2^2+2^3+....+2^{10}\)
\(2A=2+2^2+2^3+....+2^{10}+2^{11}\)
\(A=1+2+2^2+2^3+....+2^{10}\)
\(A=2^{11}-1=2047\)
b, B = 1 + 5 + 25 + 125 + ... + 15625
\(B=1+5+5^2+5^3+....+5^6\)
\(3B=5+5^2+5^3+....+5^6+5^7\)
\(B=1+5+5^2+5^3+....+5^6\)
\(2B=5^7-1\Rightarrow B=\frac{5^7-1}{2}=39062\)
d, D = 10 / 1 . 3 + 10 / 3 . 5 + 10 / 5 . 7 + ... + 10 / 2013 . 2015
\(D=\frac{10}{2}.\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{2013.2015}\right)\)
\(D=\frac{10}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{2013}-\frac{1}{2015}\right)\)
\(D=\frac{10}{2}.\left(1-\frac{1}{2015}\right)=5.\frac{2014}{2015}=\frac{2014}{403}\)
Câu c thì tương tự

\(C=\left(1+\frac{2}{3}\right).\left(1+\frac{2}{5}\right).\left(1+\frac{2}{7}\right)...\left(1+\frac{2}{2015}\right).\left(1+\frac{2}{2017}\right)\)
\(C=\frac{5}{3}.\frac{7}{5}.\frac{9}{7}...\frac{2017}{2015}.\frac{2019}{2017}\)
\(C=\frac{2019}{3}\)


a, 1/2+1/2.(-3/5)
=1/2[1+(-3/5)]
=1/2.2/5
=1/5
b,1/3-(1/3.2/3-3/9)
=1/3-(2/9-3/9)
=1/3+1/9
=4/9
c,(-2 và 1/3+1/(5/4-7/3)
=(-2/3)+(-12/13)
=-62/39
d,2015/2017.3/4+3/4.2/2017+1/4
=3/4(2015/2017+2/2017)+1/4
=3/4+1/4
=1


\(A=\left[1+\left(-2\right)\right]+\left[3+\left(-4\right)\right]+....+\left[2013+\left(-2014\right)+2015\right]\)
\(A=\left(-1\right)+\left(-1\right)+....+\left(-1\right)+2015\left(\text{1007 số hạng }\left(-1\right)\right)=1008\)