
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \((C_{15}^{12} + C_{15}^{13} )+ C_{16}^{14} = C_{16}^{13} + C_{16}^{14} = C_{17}^{14} = 680\)

a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
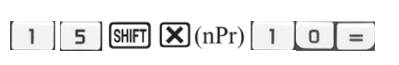
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím

Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím

Thì ta được kết quả là 1150

Tham khảo:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
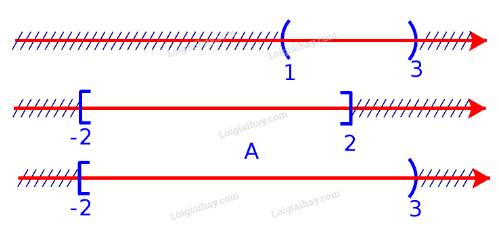
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
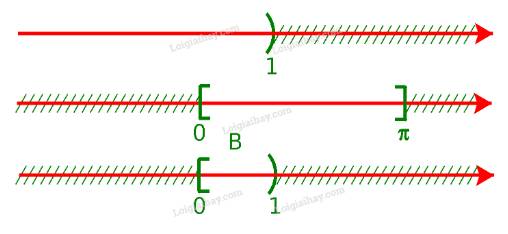
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
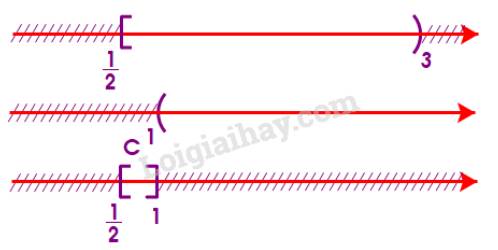
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
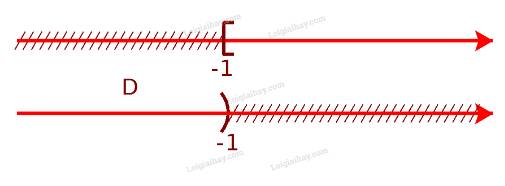
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)

Nếu đề đúng thì cả 4 đáp án đều sai nên khẳng định là đề sai
Bạn nhìn lại tập hợp A, khả năng là sai đề tại đấy :)

a: \(=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}\)
b: \(=\dfrac{6+6\cdot4+6\cdot49}{15+15\cdot4+15\cdot49}=\dfrac{6}{15}=\dfrac{2}{5}\)
c: \(=\dfrac{13\left(3-18\right)}{40\left(15-2\right)}=\dfrac{-15}{40}=-\dfrac{3}{8}\)

Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)
Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)
Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)
a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)
b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)
c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)