K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GV
Giáo viên Toán
Giáo viên
4 tháng 5 2017
a) \(\sin^4x=\left(\sin^2x\right)^2=\left(\dfrac{1-\cos2x}{2}\right)^2\)
\(=\dfrac{1}{4}\left(1-2\cos2x+\cos^22x\right)\)
\(=\dfrac{1}{4}\left(1-2.\cos2x+\dfrac{1+\cos4x}{2}\right)\)
\(=\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\)
Vậy:
\(\int\sin^4x\text{dx}=\int\left(\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\right)\text{dx}\)
\(=\dfrac{3}{8}x-\dfrac{1}{4}\sin2x+\dfrac{1}{32}\sin4x+C\)
25 tháng 12 2016
1) Đặt \(t=1+\sqrt{x-1}\Leftrightarrow x=\left(t-1\right)^2+1\forall t\ge1\Rightarrow dx=d\left(t-1\right)^2=2dt\)
\(\Rightarrow I_1=\int\frac{\left(t-1\right)^2+1}{t}\cdot2dt=2\int\frac{t^2-2t+2}{t}dt=2\int\left(t-2+\frac{2}{t}\right)dt\\ =t^2-4t+4lnt+C\)
Thay x vào ta có...
25 tháng 12 2016
2) \(I_2=\int\frac{2sinx\cdot cosx}{cos^3x-\left(1-cos^2x\right)-1}dx=\int\frac{-2cosx\cdot d\left(cosx\right)}{cos^3x+cos^2x-2}=\int\frac{-2t\cdot dt}{t^3+t-2}\)
\(I_2=\int\frac{-2t}{\left(t-1\right)\left(t^2+2t+2\right)}dt=-\frac{2}{5}\int\frac{dt}{t-1}+\frac{1}{5}\int\frac{2t+2}{t^2+2t+2}dt-\frac{6}{5}\int\frac{dt}{\left(t+1\right)^2+1}\)
Ta có:
\(\int\frac{2t+2}{t^2+2t+2}dt=\int\frac{d\left(t^2+2t+2\right)}{t^2+2t+2}=ln\left(t^2+2t+2\right)+C\)
\(\int\frac{dt}{\left(t+1\right)^2+1}=\int\frac{\frac{1}{cos^2m}}{tan^2m+1}dm=\int dm=m+C=arctan\left(t+1\right)+C\)
Thay x vào, ta có....
G
19 tháng 3 2016
a) Áp dụng đồng nhất thức \(\cos^2x+\sin^2x=1\)
ta có : \(\int\frac{1}{\cos^2x.\sin^2x}dx=\int\frac{\cos^2x+\sin^2x}{\cos^2x.\sin^2x}dx=\int\frac{dx}{\sin^2x}+\int\frac{dx}{\cos^2x}\)
\(=-\cot x+\tan x+C\)
G
19 tháng 3 2016
b) Khai triển biểu thức dưới dấu nguyên hàm ta thu được :
\(\int\left(\tan x+\cot x\right)^2dx=\int\left(\tan^2x+2+\cot^2x\right)dx\)
\(=\int\left[\left(\tan^2x+1\right)+\left(\cot^2x+1\right)\right]dx\)
\(=\int\frac{dx}{\cos^2x}+\int\frac{dx}{\sin^2x}\)
\(=\tan x-\cot x+C\)
22 tháng 3 2016
a) \(I_1=\int\frac{dx}{2\sin x\cos x}=\frac{1}{2}\int\frac{\cos x}{\sin x}.\frac{dx}{\cos^2x}\)
Đặt \(\tan x=t\)
\(=\frac{1}{2}\int\frac{dt}{t}=\frac{1}{2}\ln\left|t\right|+C=\frac{1}{2}\ln\left|\tan x\right|+C\)
b) \(I_2=\int\frac{\sin^4x}{\cos^4x}.\frac{1}{\cos^2x}.\frac{dx}{\cos^2x}\)
Đặt \(t=\tan x\)
\(=\int t^4\left(1+t^2\right)dt\)
\(=\int t^4dt+\int t^6dt=\frac{t^5}{5}+\frac{t^7}{7}+C\)
\(=\frac{\tan^5x}{5}+\frac{\tan^7x}{7}+C\)
c) \(I_3=\int\tan^3xdx\) đặt \(t=\tan x\)
\(=\int\frac{t^3}{1+t^2}dt=\int\left(t-\frac{t}{1+t^2}\right)dt\)
\(=\frac{t^2}{2}-\frac{1}{2}\ln\left(1+t^2\right)+C\)
\(=\frac{1}{2}\tan^2x+\ln\left|\cos x\right|+C\)
d) \(\int\frac{dx}{\sin^4x}=\int\frac{1}{\sin^2x}.\frac{1}{\sin^2x}dx=-\int\left(1+\cot^2x\right)d\left(\cot x\right)\)
\(=-\cot x-\frac{1}{3}\cot^3x+C\)
AH
Akai Haruma
Giáo viên
12 tháng 1 2017
Lời giải:
Câu 1:
\(A=\int\frac{dx}{1+\sin x}=\int \frac{(1-\sin x)dx}{1-\sin^2 x}=\int\frac{(1-\sin x)dx}{\cos ^2x}=\int\frac{dx}{\cos ^2x}-\int\frac{\sin x dx}{\cos^2 x}\)
\(\Leftrightarrow A=\int d(\tan x)+\int\frac{d(\cos x)}{\cos^2 x}=\tan x-\frac{1}{\cos x}+c\)
Câu 2:
\(B=\int \sin ^4 xdx=\int \sin^2 x(1-\cos ^2x)dx=\int \sin^2 xdx-\int \sin^2 x\cos^2xdx\)
Ta thấy \(\int \sin^2xdx=\frac{1}{2}\int (1-\cos 2x)dx=\frac{x}{2}-\frac{\sin 2x}{4}+c\)
Và \(\int \sin ^2x\cos^2xdx=\frac{1}{4}\int \sin^22xdx=\frac{1}{8}\int (1-\cos4x)dx=\frac{x}{8}-\frac{\sin 4x}{32}+c\)
\(\Rightarrow B=\frac{3}{8}-\frac{\sin 2x}{4}+\frac{\sin 4x}{32}+c\)
AH
Akai Haruma
Giáo viên
12 tháng 1 2017
Câu 3:
\(C=\int (\sin ^6 x+\cos^6 x)dx=\int (\sin^2x+\cos^2x)[\sin^4x-\sin^2x\cos^2x+\cos^4x)dx\)
\(\Leftrightarrow C=\int [(\sin^2x+\cos^2x)^2-3\sin^2x\cos^2x]dx\)
\(\Leftrightarrow C=\int dx-\frac{3}{4}\int\sin^22xdx=\int dx-\frac{3}{8}\int (1-\cos 4x)dx\)
\(\Leftrightarrow C=x-\frac{3x}{8}+\frac{3\sin 4x}{32}+c=\frac{5x}{8}+\frac{3\sin 4x}{32}+c\)
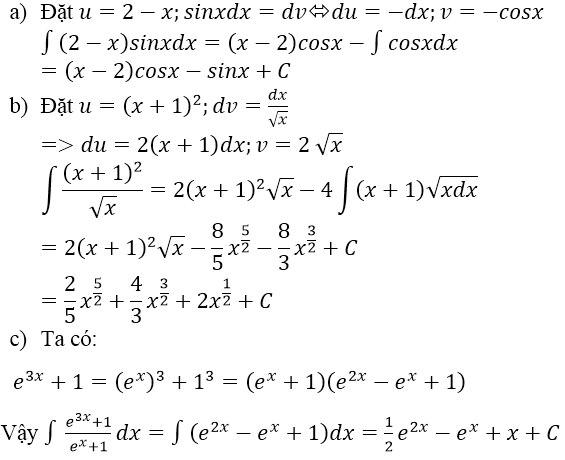
Giải như sau: Cho biểu thức cần tính là $A$
Đặt \(\begin{cases}u=x\\dv=\frac{\cos x}{\sin^3x}dx\end{cases}\) \(\Rightarrow\) \(\begin{cases}du=dx\\v=\int\frac{\cos xdx}{\sin^3x}=\int\end{cases}\frac{d\left(\sin x\right)}{\sin^3x}=\frac{-1}{2\sin^2x}}\)
Áp dụng quy tắc nguyên hàm từng phần:
\(A=-\frac{x}{2\sin^2x}+\int\frac{1}{2\sin^2x}dx=\frac{-x}{2\sin^2x}-\frac{1}{2}\int d\left(\cot x\right)=\frac{-x}{2\sin^2x}-\frac{\cot x}{2}\)
Viết lại chỗ công thức lỗi hiuhiu:
Suy ra \(d\left(u\right)=dx\) và \(v=\int\frac{\cos xdx}{\sin^3x}=\int\frac{d\left(\sin x\right)}{\sin^3x}=-\frac{1}{2\sin^2x}\)