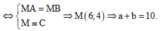K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
19 tháng 3 2017

Tính số nguyên n lớn nhất thỏa mãn  n 200 < 5 300 .

A. 10

B. 11

C. 12

D. 13
#Toán lớp 12
1
CM
Cao Minh Tâm
19 tháng 3 2017

Đúng(0)
DT
D.Công Thiện
6 tháng 8 2020

Có bao nhiêu cặp số nguyên (a; b) thỏa mãn a < 5 và hàm số f(x) = ax4 + bx3 + x2 - 3 đạt giá trị nhỏ nhất tại x=0 ?

A. 22 B. 23 C. 27 D. 26
#Toán lớp 12
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2020

- Với \(a=b=0\) thỏa mãn

- Với \(a=0;b\ne0\) hàm bậc 3 ko tồn tại min max (ko thỏa mãn)

- Với \(a< 0\Rightarrow\lim\limits_{x\rightarrow\infty}f\left(x\right)=-\infty\Rightarrow\) ko tồn tại min f(x) (loại)

\(\Rightarrow a>0\)

\(f\left(0\right)=-3\Rightarrow\) để hàm thỏa mãn yêu cầu thì \(f\left(x\right)\ge-3;\forall x\ne0\)

\(\Leftrightarrow ax^4+bx^3+x^2\ge0\Leftrightarrow x^2\left(ax^2+bx+1\right)\ge0\)

\(\Leftrightarrow ax^2+bx+1\ge0\)

\(\Leftrightarrow\Delta=b^2-4a\le0\Leftrightarrow b^2\le4a\)

- Với \(a=1\Rightarrow-2\le b\le2\) có 5 cặp

- Với \(a=2\Rightarrow-2\le b\le2\) có 5 cặp

- Với \(a=3\Rightarrow-3\le b\le3\) có 7 cặp

- Với \(a=4\Rightarrow-4\le b\le4\) có 9 cặp

Vậy tổng cộng có 27 cặp a;b thỏa mãn

Đúng(0)
PT
Pham Trong Bach
9 tháng 12 2018
Cho ba số thực dương a,b,c thỏa mãn  a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi  Q = a 2 ...
Đọc tiếp

Cho ba số thực dương a,b,c thỏa mãn  a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi  Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.

A. 10

B. -10

C. 12

D. -12
#Toán lớp 12
1
CM
Cao Minh Tâm
9 tháng 12 2018

Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu  (S) và mặt phẳng (P) sao cho KM lớn nhất

Đúng(0)
PT
Pham Trong Bach
29 tháng 11 2018
Cho các số thực a,b,c thỏa mãn . Tính P = a+ 2b+ 3c khi biểu thức 2 a + b - 2 c + 7 đạt giá trị lớn nhất  A. P=7 B. P=3 C. P=-3 D. P=-7...
Đọc tiếp

Cho các số thực a,b,c thỏa mãn . Tính P = a+ 2b+ 3c khi biểu thức 2 a + b - 2 c + 7 đạt giá trị lớn nhất 

A. P=7

B. P=3

C. P=-3

D. P=-7
#Toán lớp 12
1
CM
Cao Minh Tâm
29 tháng 11 2018

Đáp án B

Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:

2 a + b - 2 c + 7 = 2 a + 1 + b - 2 - 2 c + 11 ≤ 2 a - 1 + b - 2 - 2 c + 11 ≤ a - 1 2 + b - 2 2 + c 2 2 2 + 1 2 + - 2 2 + 11 = 20

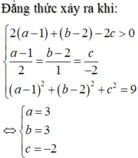
Cách 2: phương pháp hình học.

Trong không gian Oxyz, gọi mặt cầu (S) có tâm I(1;2;0), bán kính R=3. Khi đó:

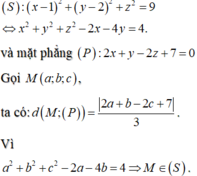
Bài toán đã cho trở thành:

Tìm  M ∈ ( S )  sao cho d(M;(P)) lớn nhất

Gọi △  là đường thẳng qua I và vuông góc (P)

Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết kiệm thời gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS. Đối với Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những bước tính toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng không mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của biểu thức  2 a + b - 2 c + 7

 

 

Đúng(0)
NT
Nguyễn thị Phụng
12 tháng 10 2020
Câu 1 : Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = \(\frac{3sinx+2}{sinx+1}\) trên đoạn \(\left[0;\frac{\Pi}{2}\right]\) . Khi đó giá trị của \(M^2+m^2\) là A. \(\frac{31}{2}\) B. \(\frac{11}{2}\) C. \(\frac{41}{4}\) D. \(\frac{61}{4}\) Câu 2 : Gọi M , N lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = \(x+\sqrt{4-x^2}\) . giá trị...
Đọc tiếp

Câu 1 : Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = \(\frac{3sinx+2}{sinx+1}\) trên đoạn \(\left[0;\frac{\Pi}{2}\right]\) . Khi đó giá trị của \(M^2+m^2\) là

A. \(\frac{31}{2}\) B. \(\frac{11}{2}\) C. \(\frac{41}{4}\) D. \(\frac{61}{4}\)

Câu 2 : Gọi M , N lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = \(x+\sqrt{4-x^2}\) . giá trị của biểu thức ( M + 2N ) là

A. \(2\sqrt{2}+2\) B. \(4-2\sqrt{2}\) C. \(2\sqrt{2}-4\) D. \(2\sqrt{2}-2\)

Câu 3 : Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số y = \(-x^3-3x^2+m\) trên đoạn \(\left[-1;1\right]\) bằng 0

A. m = 0 B. m = 6 C. m = 2 D. m = 4

Câu 4 : Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = \(\frac{x+m}{x+1}\) trên \(\left[1;2\right]\) bằng 8 ( m là tham số thực ) . Khẳng định nào sau đây đúng ?

A. m > 10 B. 8 < m < 10 C. 0 < m < 4 D. 4 < m < 8

#Toán lớp 12
2
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020

3.

\(y'=-3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)

\(y\left(-1\right)=m-2\) ; \(y\left(1\right)=m-4\)

\(\Rightarrow y_{min}=y\left(1\right)=m-4\)

\(\Rightarrow m-4=0\Rightarrow m=4\)

4.

Hàm đã cho bậc nhất trên bậc nhất nên đơn điệu trên mọi khoảng xác định

\(\Rightarrow y_{min}+y_{max}=y\left(1\right)+y\left(2\right)=\frac{m+1}{2}+\frac{m+2}{3}=8\)

\(\Rightarrow m=\frac{41}{5}\)

Đáp án B

Đúng(0)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 10 2020

1.

\(y'=\frac{1}{\left(sinx+1\right)^2}.cosx>0\Rightarrow y\) đồng biến

\(m=y_{min}=y\left(0\right)=2\)

\(M=y_{max}=y\left(1\right)=\frac{5}{2}\)

\(\Rightarrow M^2+m^2=\frac{41}{4}\)

2.

Hàm xác định trên \(\left[-2;2\right]\)

\(y'=1-\frac{x}{\sqrt{4-x^2}}=0\Leftrightarrow x=\sqrt{2}\)

\(y\left(-2\right)=-2\) ; \(y\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(y\left(2\right)=2\)

\(\Rightarrow N=-2;M=2\sqrt{2}\)

\(\Rightarrow M+2N=2\sqrt{2}-4\)

Đúng(0)
PT
Pham Trong Bach
21 tháng 1 2017
Giả sử a,b,c là các số nguyên thỏa mãn ∫ 0 4 2 x 2 + 4 x + 1 2 x + 1 d x   =   1 2 ...
Đọc tiếp

Giả sử a,b,c là các số nguyên thỏa mãn ∫ 0 4 2 x 2 + 4 x + 1 2 x + 1 d x   =   1 2 ∫ 1 3 ( a u 4 + b u 2 + c ) d u , trong đó u   =   2 x + 1 . Tính giá trị S=a+b+c

A. S = 3

B. S = 0

C. S = 1

D. S = 2
#Toán lớp 12
1
CM
Cao Minh Tâm
21 tháng 1 2017

Đáp án D

Đúng(0)
TT
Thủy Tiên
26 tháng 5 2018

trong không gian Oxyz, cho hai điểm A(-2;2;-2), B(3;-3;3). Điểm M trong không gian thỏa mãn \(\dfrac{MA}{MB}=\dfrac{2}{3}\). Khi đó độ dài OM lớn nhất bằng:

A.6√3 B. 12√3 C. \(\dfrac{5\sqrt{3}}{2}\) D. 5√3
#Toán lớp 12
1
CT
chu thị ánh nguyệt
28 tháng 5 2018

tọa độ điểm M thỏa mãn j v

Đúng(0)
PT
Pham Trong Bach
22 tháng 2 2018

Tìm số nguyên n lớn nhất thỏa mãn n360 < 3480

A. n = 3

B. n = 4

C. n = 2

D. n = 5
#Toán lớp 12
1
CM
Cao Minh Tâm
22 tháng 2 2018

Đáp án B

Ta có

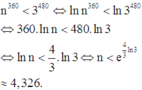
Vậy giá trị nguyên n lớn nhất thỏa mãn là n = 4

Đúng(0)
PT
Pham Trong Bach
11 tháng 11 2017

Xét các số phức z = a +  bi(a,b ∈ ℝ ) thỏa mãn điều kiện |z - 4 - 3i| = 5 . Tính P = a + b khi giá trị biểu thức |z + 1 - 3i + |z - 1 + i|| đạt giá trị lớn nhất.

A. P = 10

B. P = 4

D. P = 6

D. P = 8
#Toán lớp 12
1
CM
Cao Minh Tâm
11 tháng 11 2017

Đáp án A

Gọi M(x;y) là điểm biều diễn số phức z.

Từ giả thiết, ta có |z - 4 - 3i| = 5  

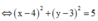
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =   5

Khi đó P = MA + MB với A(-1;3), B(1;-1)

Ta có

Gọi E(0;1) là trung điểm của AB 

Do đó  mà  suy ra 

 

Với C là giao điểm của đường thẳng EI với đường tròn (C)

Vậy Dấu “=”xảy ra  

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP