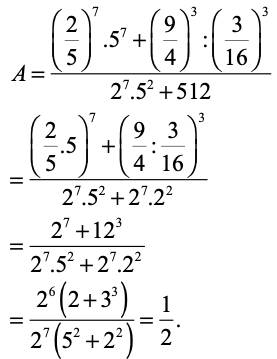Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{16^7\cdot5^3\left(5-1\right)}{16^7\cdot\left(25^2-5^3\right)}=\dfrac{5^3\cdot2^2}{5^4-5^3}=\dfrac{5^3\cdot2^2}{5^3\cdot\left(5-1\right)}=1\)

\(a,=\dfrac{3^6\cdot5^4\cdot9^4-5^{13}\cdot3^{13}\cdot5^{-9}}{3^{12}\cdot5^6+9^6\cdot5^6}=\dfrac{3^{14}\cdot5^4-5^4\cdot3^{13}}{3^{12}\cdot5^6+3^{12}\cdot5^6}\\ =\dfrac{3^{13}\cdot5^4\cdot2}{2\cdot3^{12}\cdot5^6}=\dfrac{3}{5^2}=\dfrac{3}{25}\)
\(b,=\dfrac{\left(\dfrac{2}{5}\cdot5\right)^7+\left(\dfrac{9}{4}\cdot\dfrac{16}{3}\right)^3}{2^7\cdot5^2+2^9}=\dfrac{2^7+12^3}{2^7\left(5^2+2^2\right)}=\dfrac{2^7+4^3\cdot3^3}{2^7\cdot29}=\dfrac{2^6\left(2+3^3\right)}{2^7\cdot29}=\dfrac{1}{2}\)

\(A=\dfrac{\left(\dfrac{2}{5}\right)^7.5^7+\left(\dfrac{9}{4}\right)^3:\left(\dfrac{3}{16}\right)^3}{2^7.5^2+512}\\ A=\dfrac{128+1728}{153+512}\\ A=\dfrac{1856}{665}=2\dfrac{526}{665}\)
Chúc bạn học tốt!!!![]()
\(\dfrac{\left(\dfrac{2}{5}\right)^7\cdot5^7+\left(\dfrac{9}{4}\right)^3:\left(\dfrac{3}{16}\right)^3}{2^7+5^2+512}\)

Bạn đổi \(\left(\frac{2}{5}\right)^7.5^7=\frac{2^7}{5^7}.5^7=2^7=128\)
\(\left(\frac{9}{4}\right)^3:\left(\frac{3}{16}\right)^3=\frac{9^3}{4^3}.\frac{16^3}{3^3}=\frac{3^3.3^3}{4^3}.\frac{4^3.4^3}{3^3}=3^3.4^3=17.64=1088\)
CỘNG 2 CÁI ĐÓ LẠI RỒI LÀM Ở TỬ SỐ LÀ RA.
BẤM ĐÚNG NẾU THẤY ĐÚNG
\(=\frac{\left(\frac{2}{5}.5\right)^7+\left(\frac{9}{4}:\frac{3}{16}\right)^3}{2^7.5^2+512}=\frac{2^7+12^3}{2^7.5^2+512}=\frac{128+1728}{3200+512}=\frac{1856}{3712}=\frac{1}{2}\)