
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2}.\frac{1}{2}+\frac{1}{2}.\frac{1}{3}\)\(+\frac{1}{3}.\frac{1}{4}+\frac{1}{4}.\frac{1}{5}+\frac{1}{5}.\frac{1}{6}\)
\(=\frac{1}{4}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}\)
\(=\frac{1}{4}+\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}\right)\)
\(=\frac{1}{4}+\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}\right)\)
\(=\frac{1}{4}+\left(\frac{1}{2}-\frac{1}{6}\right)\)
\(=\frac{1}{4}+\frac{1}{3}\)
\(=\frac{7}{12}\)

Bài 2:
\(=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{999\cdot1000}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{999}-\dfrac{1}{1000}\)
=1-1/1000
=999/1000

3) Ta có : \(A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+.....+\frac{2}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+.....+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)
4)
A = \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{99.101}\)
A = \(\frac{1}{2}.\left(1-\frac{1}{3}\right)+\frac{1}{2}.\left(\frac{1}{3}-\frac{1}{5}\right)+\frac{1}{2}.\left(\frac{1}{5}-\frac{1}{7}\right)+...+\frac{1}{2}.\left(\frac{1}{99}-\frac{1}{101}\right)\)
A = \(\frac{1}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{99}-\frac{1}{101}\right)\)
A = \(\frac{1}{2}.\left(1-\frac{1}{101}\right)\)
\(A=\frac{1}{2}.\frac{100}{101}\)
A = \(\frac{50}{101}\)
2, đặt tên biểu thức trên là A. Ta có :
\(A=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{10100}\)
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{100.101}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{100}-\frac{1}{101}\)
\(A=1-\frac{1}{101}\)
\(A=\frac{100}{101}\)
1) \(\frac{1}{1}.\frac{1}{2}+\frac{1}{2}.\frac{1}{3}+\frac{1}{3}.\frac{1}{4}+\frac{1}{4}.\frac{1}{5}\)
= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}\)
\(=1-\frac{1}{5}\)
\(=\frac{4}{5}\)

S = 1/1x1/2+1/2x1/3+1/3x1/4+...+1/28x1/29+1/29+1/30
S = 1/1-1/2+1/2-1/3+1/3-1/4+...+1/28-1/29+1/29+1/30
Đến đây ta triệt tiêu,còn lại:
S = 1/1-1/30
S = 29/30
Mình chắc chắn lun!
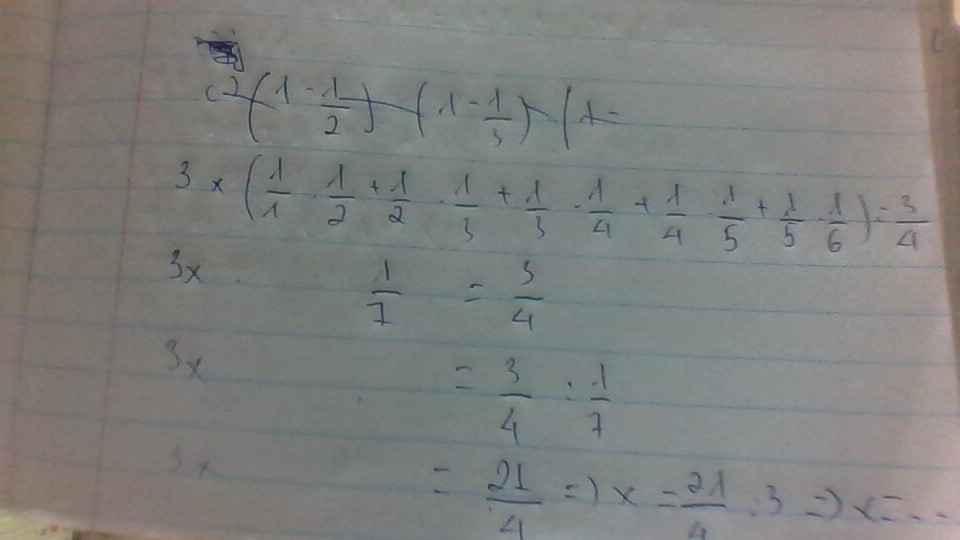
999/1000
1/1.2+1/2.3+1/3.4+1/4.5+.................+1/9990999.9991000
=1-1/2+1/2-1/3+1/3-1/4+1/4-1/5+.................+1/9990999-1/9991000
=1-1/9991000
=9990999/9991000