Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\Leftrightarrow xy+yz+xz=0\)
\(A=\frac{yz}{x^2+yz+-xy-xz}+\frac{xz}{y^2+zx-xy-yz}+\frac{xy}{z^2+xy-xz-yz}\)
\(A=\frac{yz}{\left(x-y\right)\left(x-z\right)}+\frac{xz}{\left(y-z\right)\left(y-x\right)}+\frac{xy}{\left(z-x\right)\left(z-y\right)}\)
\(A=\frac{yz\left(y-z\right)-xz\left(x-z\right)+xy\left(x-y\right)}{\left(x-z\right)\left(x-y\right)\left(y-z\right)}\)
\(A=\frac{\left(z-x\right)\left(y-z\right)\left(y-x\right)}{\left(x-z\right)\left(x-y\right)\left(y-z\right)}=1\)

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
Suy ra xy+yz+zx=0
Ta có: \(x^2+2yz=x^2+yz+yz=x^2+yz-xy-xz=\left(x-y\right)\left(x-z\right)\)
tương tự \(y^2+2xz=\left(y-z\right)\left(y-x\right)\)
\(z^2+2xy=\left(z-x\right)\left(z-y\right)\)
thay vào A ta được:
\(A=\dfrac{yz}{\left(x-y\right)\left(x-z\right)}+\dfrac{xz}{\left(y-z\right)\left(y-x\right)}+\dfrac{xy}{\left(z-y\right)\left(z-x\right)}\)
\(A=-\dfrac{xy\left(x-y\right)+yz\left(y-z\right)+zx\left(z-x\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\)
\(A=\dfrac{\left(x-y\right)\left(y-z\right)\left(z-x\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=1\)

Ta có \(\frac{x+2xy+1}{x+xy+xz+1}=\frac{x+2xy+xyz}{x+xy+xz+xyz}=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}\)
Tương tự => \(M=\frac{1+2y+yz}{\left(y+1\right)\left(z+1\right)}+\frac{1+2z+zx}{\left(1+x\right)\left(z+1\right)}+\frac{1+2x+xy}{\left(1+x\right)\left(y+1\right)}\)
=> \(M=\frac{\left(1+2y+yz\right)\left(1+x\right)+\left(1+2z+zx\right)\left(1+y\right)+\left(1+2x+xy\right)\left(1+z\right)}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
=>\(M=\frac{6+3\left(x+y+z\right)+3\left(xy+yz+xz\right)}{2+\left(x+y+z\right)+\left(xy+yz+xz\right)}=3\)

Lời giải:
Ta xét hiệu sau:
\(x^3+y^3-xy(x+y)=x^3-x^2y-(xy^2-y^3)\)
\(=x^2(x-y)-y^2(x-y)=(x^2-y^2)(x-y)=(x-y)^2(x+y)\geq 0, \forall x,y>0\)
\(\Rightarrow x^3+y^3\geq xy(x+y)(*)\)
\(\Rightarrow x^3+y^3+xy\geq xy(x+y+1)\)
\(\Rightarrow \frac{xy}{x^3+y^3+xy}\leq \frac{xy}{xy(x+y+1)}=\frac{1}{x+y+1}\)
Hoàn toàn tương tự với các phân thức còn lại và cộng theo vế, suy ra:
\(\text{VT}\leq \underbrace{\frac{1}{x+y+1}+\frac{1}{y+z+1}+\frac{1}{x+z+1}}_{M}(1)\)
Vì $xyz=1$ nên tồn tại $a,b,c>0$ sao cho \((x,y,z)=(\frac{a^2}{bc}, \frac{b^2}{ac}, \frac{c^2}{ab})\)
Khi đó:
\(M=\frac{abc}{a^3+b^3+abc}+\frac{abc}{b^3+c^3+abc}+\frac{abc}{c^3+a^3+abc}\)
\(\leq \frac{abc}{ab(a+b)+abc}+\frac{abc}{bc(b+c)+abc}+\frac{abc}{ca(c+a)+abc}\) (áp dụng công thức $(*)$)
hay \(M\leq \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c}=\frac{a+b+c}{a+b+c}=1(2)\)
Từ \((1);(2)\Rightarrow \text{VT}\leq 1\) (đpcm)
Dấu "=" xảy ra khi $a=b=c$ hay $x=y=z=1$
Bài của chị Akai đoạn đầu hơi phức tạp(em nghĩ thế).
Ta có:
\(\left(x-y\right)^2\ge0\) với \(\forall x,y\)
\(\Rightarrow x^2+y^2-xy\ge0\) với \(\forall x,y\)
\(\Rightarrow\left(x+y\right)\left(x^2-xy+y^2\right)\ge xy\left(x+y\right)\)với\(\forall x,y\)
\(\Rightarrow x^3+y^3\ge xy\left(x+y\right)\) với \(\forall x,y\)
Rồi giải tiếp như chị ấy.

Lời giải:
Từ \(xy+yz+xz=xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
Đặt \((a,b,c)=\left(\frac{1}{x}; \frac{1}{y}; \frac{1}{z}\right)\Rightarrow a+b+c=1\)
BĐT cần chứng minh trở thành:
\(P=\frac{c^3}{(a+1)(b+1)}+\frac{a^3}{(b+1)(c+1)}+\frac{b^3}{(c+1)(a+1)}\geq \frac{1}{16}(*)\)
Thật vậy, áp dụng BĐT Cauchy ta có:
\(\frac{c^3}{(a+1)(b+1)}+\frac{a+1}{64}+\frac{b+1}{64}\geq 3\sqrt[3]{\frac{c^3}{64^2}}=\frac{3c}{16}\)
\(\frac{a^3}{(b+1)(c+1)}+\frac{b+1}{64}+\frac{c+1}{64}\geq 3\sqrt[3]{\frac{a^3}{64^2}}=\frac{3a}{16}\)
\(\frac{b^3}{(c+1)(a+1)}+\frac{c+1}{64}+\frac{a+1}{64}\geq 3\sqrt[3]{\frac{b^3}{64^2}}=\frac{3b}{16}\)
Cộng theo vế các BĐT trên và rút gọn :
\(\Rightarrow P+\frac{a+b+c+3}{32}\geq \frac{3(a+b+c)}{16}\)
\(\Leftrightarrow P+\frac{4}{32}\geq \frac{3}{16}\Leftrightarrow P\geq \frac{1}{16}\)
Vậy \((*)\) được chứng minh. Bài toán hoàn tất.
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{3}\Leftrightarrow x=y=z=3\)

Lời giải:
Ta có: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\Leftrightarrow xy+yz+xz=xyz\)
\(\Rightarrow x^2+xy+yz+xz=x^2+xyz=x(x+yz)\)
\(\Leftrightarrow x+yz=\frac{x^2+xy+yz+xz}{x}=\frac{(x+y)(x+z)}{x}\)
\(\Rightarrow \sqrt{x+yz}=\sqrt{\frac{(x+y)(x+z)}{x}}\)
Áp dụng BĐT Bunhiacopxky:\((x+y)(x+z)\geq (x+\sqrt{yz})^2\)
\(\Rightarrow \sqrt{x+yz}=\sqrt{\frac{(x+y)(x+z)}{x}}\geq \frac{x+\sqrt{yz}}{\sqrt{x}}\)
Hoàn toàn tương tự:
\(\sqrt{y+xz}\geq \frac{y+\sqrt{xz}}{\sqrt{y}}\); \(\sqrt{z+xy}\geq \frac{z+\sqrt{xy}}{\sqrt{z}}\)
Cộng theo vế các BĐT đã thu được ta có:
\(\text{VT}\geq \frac{x+\sqrt{yz}}{\sqrt{x}}+\frac{y+\sqrt{xz}}{\sqrt{y}}+\frac{z+\sqrt{xy}}{\sqrt{z}}=\sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{xy+yz+xz}{\sqrt{xyz}}\)
\(\Leftrightarrow \text{VT}\geq \sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{xyz}{\sqrt{xyz}}=\sqrt{x}+\sqrt{y}+\sqrt{z}+\sqrt{xyz}=\text{VP}\)
Do đó ta có đpcm.
Dấu bằng xảy ra khi \(x=y=z=3\)
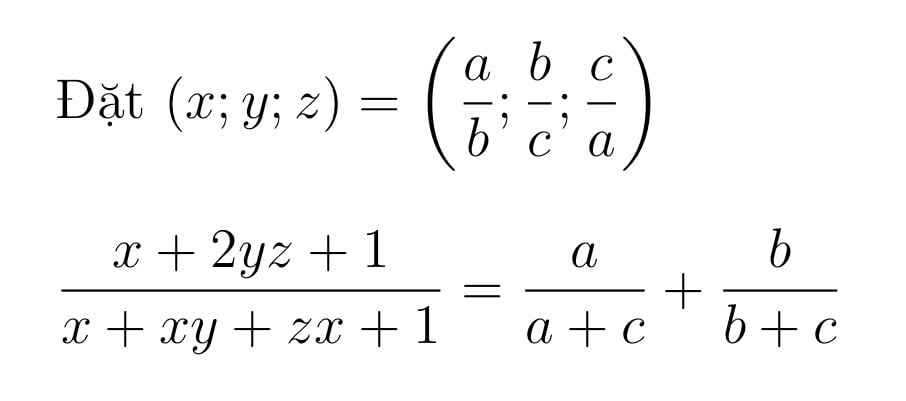
\(B=\dfrac{x+2xy+1}{x+xy+xz+1}+\dfrac{y+2yz+1}{y+yz+ỹ+1}+\dfrac{z+2zx+1}{z+zx+zy+1}\)
\(B=\dfrac{yz\left(x+2xy+1\right)}{yz\left(x+xy+xz+1\right)}+\dfrac{xz\left(y+2yz+1\right)}{xz\left(y+yz+ỹ+1\right)}+\dfrac{xy\left(z+2zx+1\right)}{xy\left(z+zx+zy+1\right)}\)
\(B=\dfrac{\left(1+y\right)+y\left(1+z\right)}{\left(1+y\right)\left(1+z\right)}+\dfrac{\left(1+z\right)+z\left(1+x\right)}{\left(1+z\right)\left(1+x\right)}+\dfrac{\left(1+x\right)+x\left(1+y\right)}{\left(1+x\right)\left(1+y\right)}\)
\(B=\dfrac{y}{1+y}+\dfrac{1}{1+z}+\dfrac{1}{1+x}+\dfrac{z}{1+z}+\dfrac{1}{1+y}+\dfrac{x}{1+x}\)
\(B=\left(\dfrac{y}{1+y}+\dfrac{1}{1+y}\right)+\left(\dfrac{1}{1+z}+\dfrac{z}{1+z}\right)+\left(\dfrac{x}{1+x}+\dfrac{1}{1+x}\right)\)
\(B=1+1+1\)
\(B=3\)