Question

[Linh Trần]

Tính giới hạn của dãy số \(u_n=q+2q^2+3q^3+...+nq^n\) với \(\left|q\right|< 1\)

Answer 1

[Hoàng Tử Hà]

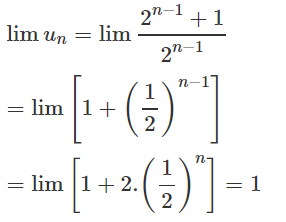
Nếu ở hệ số ở mũ 2 là 1 có khi xài đạo hàm chút là ra tổng quát, còn cái này thì...khó :D

Gọi q là k đi, máy tui kẹt chữ q, xài On-screen keyboard mệt lắm

\(u_n=k+2k^2+3k^3+...+nk^n\)

Nhận thấy nếu giờ chia k cho un thì sẽ có \(1+2k+3k+...+nk^{n-1}\), ta đã đưa về dạng tổng quát có thể đạo hàm được, sau đó chỉ cần nhân k là ra un

\(\dfrac{u_n}{k}=1+2k+3k^2+...+nk^{n-1}\)

\(f\left(x\right)=1+k+k^2+...+k^n\)

\(\left\{{}\begin{matrix}u_1=1\\q=k\end{matrix}\right.\Rightarrow f\left(x\right)=1.\dfrac{q^{n+1}-1}{q-1}=\dfrac{k^{n+1}-1}{k-1}\)

Dao ham 2 ve: 

\(\Rightarrow f'\left(x\right)=1+2k+3k^2+...+nk^{n-1}=\dfrac{\left(k^{n+1}-1\right)'\left(k-1\right)-\left(k-1\right)'\left(k^{n+1}-1\right)}{\left(k-1\right)^2}\)

\(\Leftrightarrow f'\left(x\right)=\dfrac{\left(n+1\right)k^n\left(k-1\right)-k^{n+1}+1}{\left(k-1\right)^2}\)

\(f'\left(x\right)=\dfrac{k^n\left[\left(n+1\right)\left(k-1\right)-k\right]+1}{\left(k-1\right)^2}\)

\(\Rightarrow f'\left(x\right)=\dfrac{u_n}{k}\Rightarrow u_n=f'\left(x\right).k=\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}\)

\(\Rightarrow lim\left(u_n\right)=lim\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}=\lim\limits\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]}{\left(k-1\right)^2}+\dfrac{k}{\left(k-1\right)^2}\)

\(\left|k\right|< 1\Rightarrow lim\left(k^{n+1}\right)=0\)

\(\Rightarrow\lim\limits\left(u_n\right)=\dfrac{k}{\left(k-1\right)^2}\)

P/s: Một cách làm rất mới mẻ, có thể tổng quát cho nhiều bài toàn sinh ra từ dãy số vừa rồi :D

Answer 2

[Akai Haruma]

Lời giải:

\(u_n=q+2q^2+3q^3+...+nq^n\)

\(qu_n=q^2+2q^3+3a^4+...+nq^{n+1}\)

\(\Rightarrow u_n(1-q)=q+q^2+q^3+...+q^n-nq^{n+1}\)

\(\Leftrightarrow u_n(1-q)=q.\frac{q^n-1}{q-1}-nq^{n+1}\)

\(\Leftrightarrow u_n=q.\frac{1-q^n}{(1-q)^2}+\frac{nq^{n+1}}{q-1}=\frac{q-q^{n+1}}{(1-q)^2}+\frac{nq^{n+1}}{q-1}\)

Vì $|q|< 1$ nên $\lim\limits q^{n+1}=0$ nên $\lim\limits u_n=\frac{q}{(1-q)^2}$