Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+\dfrac{5^2}{11.16}+...+\dfrac{5^2}{96.101}\\ S=\dfrac{25}{1.6}+\dfrac{25}{6.11}+\dfrac{25}{11.16}+...+\dfrac{25}{96.101}\\ S=5.\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+...+\dfrac{5}{96.101}\right)\\ S=5.\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{96}-\dfrac{1}{101}\right)\\ S=5.\left(1-\dfrac{1}{101}\right)\\ S=5.\dfrac{100}{101}\\ S=\dfrac{500}{101}\)

a, \(A=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+...+\dfrac{5^2}{26.31}\)
\(A=5.\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+...+\dfrac{5}{26.31}\right)\)
\(A=5.\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
(do \(\dfrac{n}{a\left(a+n\right)}=\dfrac{1}{a}-\dfrac{1}{a+n}\) với \(a\in N\)*)
\(A=5.\left(1-\dfrac{1}{31}\right)=5.\dfrac{30}{31}=\dfrac{150}{31}\)
b, \(B=\dfrac{6}{15.18}+\dfrac{6}{18.21}+...+\dfrac{6}{87.90}\)
\(B=2\left(\dfrac{3}{15.18}+\dfrac{3}{18.21}+...+\dfrac{13}{87.90}\right)\)
\(B=2\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
(do \(\dfrac{n}{a\left(a+n\right)}=\dfrac{1}{a}-\dfrac{1}{a+n}\) với \(a\in N\)*)
\(B=2\left(\dfrac{1}{15}-\dfrac{1}{90}\right)=2.\dfrac{1}{18}=\dfrac{1}{9}\)
c, \(C=\dfrac{3^2}{8.11}+\dfrac{3^2}{11.14}+...+\dfrac{3^2}{197.200}\)
\(C=3\left(\dfrac{3}{8.11}+\dfrac{3}{11.14}+...+\dfrac{3}{197.200}\right)\)
\(C=3\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)
(do \(\dfrac{n}{a\left(a+n\right)}=\dfrac{1}{a}-\dfrac{1}{a+n}\) với \(a\in N\)*)
\(C=3\left(\dfrac{1}{8}-\dfrac{1}{200}\right)=3.\dfrac{3}{35}=\dfrac{9}{35}\)
Chúc bạn học tốt!!!

ính giá trị của các biểu thức sau:
A=827−(349+427)A=827−(349+427)
B=(1029+235)−629B=(1029+235)−629
Giải:
A=827−(349+427)A=827−(349+427)
=587−(319+307)=58−307−319=4−319=587−(319+307)=58−307−319=4−319
= 36−319=5936−319=59
B=(1029+235)−629B=(1029+235)−629
=1029−629+235=4+235=635
ính giá trị của các biểu thức sau:
A
=
8
2
7
−
(
3
4
9
+
4
2
7
)
A=827−(349+427)
B
=
(
10
2
9
+
2
3
5
)
−
6
2
9
B=(1029+235)−629
Giải:
A
=
8
2
7
−
(
3
4
9
+
4
2
7
)
A=827−(349+427)
=
58
7
−
(
31
9
+
30
7
)
=
58
−
30
7
−
31
9
=
4
−
31
9
=587−(319+307)=58−307−319=4−319
=
36
−
31
9
=
5
9
36−319=59
B
=
(
10
2
9
+
2
3
5
)
−
6
2
9
B=(1029+235)−629
=
10
2
9
−
6
2
9
+
2
3
5
=
4
+
2
3
5
=
6
3
5
Xem thêm tại: http://loigiaihay.com/bai-100-trang-47-sgk-toan-6-tap-2-c41a24737.html#ixzz4eUGN0ooE

\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-16}{10}:\dfrac{5}{3}\)
\(A=\dfrac{-8}{5}.\dfrac{3}{5}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)
\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\dfrac{5}{3}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)

A = \(\dfrac{\dfrac{2}{3}+\dfrac{2}{5}-\dfrac{2}{9}}{\dfrac{4}{3}+\dfrac{4}{5}-\dfrac{4}{9}}\)
A = \(\dfrac{\dfrac{2}{3}+\dfrac{2}{5}-\dfrac{2}{9}}{2.\left(\dfrac{2}{3}+\dfrac{2}{5}-\dfrac{2}{9}\right)}=\dfrac{1}{2}\)

P= \(\dfrac{3}{1.6}\)+\(\dfrac{3}{6.11}\)+\(\dfrac{3}{11.17}\)+...+\(\dfrac{3}{96.101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{5}{3}\).(\(\dfrac{3}{1.6}\)+\(\dfrac{3}{6.11}\)+\(\dfrac{3}{11.16}\)+...+\(\dfrac{3}{96.101}\))
\(\dfrac{5}{3}\).P= \(\dfrac{5}{1.6}\)+\(\dfrac{5}{6.11}\)+\(\dfrac{5}{11.16}\)+...+\(\dfrac{5}{96.101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{1}{1}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{11}\)+\(\dfrac{1}{11}\)-\(\dfrac{1}{16}\)+...+\(\dfrac{1}{96}\)-\(\dfrac{1}{101}\)
\(\dfrac{5}{3}\).P= \(\dfrac{1}{1}\)-\(\dfrac{1}{101}\)= \(\dfrac{101}{101}\)-\(\dfrac{1}{101}\)=\(\dfrac{100}{101}\)
P= \(\dfrac{100}{101}\):\(\dfrac{5}{3}\)= \(\dfrac{100}{101}\).\(\dfrac{3}{5}\)=\(\dfrac{100.3}{101.5}\)=\(\dfrac{20.3}{101.1}\)=\(\dfrac{60}{101}\)
Vậy P= \(\dfrac{60}{101}\)

A=1/15-1/16+1/16-1/17+...+1/2016-1/2017
A=1/15-1/2017
A=2002/30255
C=1/3[3/5.8+3/8.11+...+3/101.104]
C=1/3[1/5-1/8+1/8-1/11+...+1/101-1/104]
C=1/3[1/5-1/104]
C=1/3.99/520
C=33/520
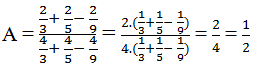
`A = ( 5^2 )/( 1*6)+(5^2)/(6*11)+.....+(5^2)/(26*31)`
`= 5*( 5/( 1*6)+ 5/(6*11)+.....+5/(26*31))`
`= 5*( 1 - 1/6 + 1/6 - 1/11 +....+1/26 - 1/31 )`
`= 5*( 1 - 1/31 )`
`= 5 * 30/31 = 150/31`
\(A=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+...+\dfrac{5^2}{26.31}\)
\(=5.\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+...+\dfrac{5}{26.31}\right)\)
\(=5.\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
\(=5.\left(1-\dfrac{1}{31}\right)=5.\dfrac{30}{31}=\dfrac{150}{31}\)