Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(A=\left(x-y\right)\left(x^2+xy+y^2\right)+2y^3\)
\(A=x^3-y^3+2y^3\)
\(A=x^3+y^3\)
Thay \(x=\dfrac{2}{3},y=\dfrac{1}{3}\) vào A, ta có:
\(A=\left(\dfrac{2}{3}\right)^3+\left(\dfrac{1}{3}\right)^3=\dfrac{8}{27}+\dfrac{1}{27}=\dfrac{9}{27}=\dfrac{1}{3}\)

Câu 1:
\(\dfrac{2^{35}.45^{25}.13^{22}.35^{16}}{9^{26}.65^{22}.28^{17}.25^9}\)
\(=\dfrac{2^{35}.9^{25}.5^{25}.13^{22}.7^{16}.5^{16}}{9^{26}.13^{22}.5^{22}.2^{17}.2^{17}.7^{17}.5^9.5^9}\)
Bạn rút gọn sẽ còn lại:
\(=\dfrac{2.5}{7.9}=\dfrac{10}{63}\)
Câu 4:
\(K=\left(x^2y-3\right)^2-\left(2x-y\right)^3+xy^2\left(6-x^3\right)+8x^3-6x^2y-y^3\)\(K=\left(x^2y\right)^2-2.x^2y.3+3^2-\left[\left(2x\right)^3-3.\left(2x\right)^2.y+3.2x.y^2-y^3\right]+6xy^3-x^4y^2+8x^3-6x^2y-y^3\)\(K=x^4y^2-6x^2y+9-8x^3+12x^2y-6xy^2+y^3+6xy^2-x^4y^2+8x^3-6x^2y-y^3\)\(K=9\)

1, \(25x^2-10xy+y^2=\left(5x-y\right)^2\)
2, \(8x^3+36x^2y+54xy^2+27y^3=\left(2x+3y\right)^3\)
4, \(\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)-a^3-b^3-c^3\)
\(=3\left(a+b\right)\left(b+c\right)\left(a+c\right)\)
5, \(2x^3+3x^2+2x+3\)
\(=x^2\left(2x+3\right)+2x+3\)
\(=\left(x^2+1\right)\left(2x+3\right)\)
6, \(x^3z+x^2yz-x^2z^2-xyz^2\)
\(=x^3z-x^2z^2+x^2yz-xy^2\)
\(=xz\left(x^2-xz\right)+xz\left(xy-yz\right)\)
\(=xz\left[x\left(x-z\right)+y\left(x-z\right)\right]\)
\(=xz\left(x+y\right)\left(x-z\right)\)
8, \(x^3+3x^2y+3xy^2+y+y^3\)\(=\left(x+y\right)^3+y\)
9, \(x^2-6x+8\)
\(=x^2-4x-2x+8\)
\(=x\left(x-4\right)-2\left(x-4\right)\)
\(=\left(x-2\right)\left(x-4\right)\)
10, \(x^2-8x+12\)
\(=x^2-6x-2x+12\)
\(=x\left(x-6\right)-2\left(x-6\right)\)
\(=\left(x-2\right)\left(x-6\right)\)
Chỗ còn lại mai làm nốt nha.
Gặp chút sự cố đăng nhập nên hơi muộn, xin lỗi nha
11, \(a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)\)
\(=a^2b-a^2c+b^2c-b^2a+c^2a-c^2b\)
\(=a^2b-ab^2+abc-a^2c+b^2c-abc+ac^2-c^2b\)
\(=ab\left(a-b\right)-ac\left(a-b\right)-bc\left(a-b\right)+c^2\left(a-b\right)\)
\(=\left(a-b\right)\left(ab-ac-bc+c^2\right)\)
\(=\left(a-b\right)\left[b\left(a-c\right)-c\left(a-c\right)\right]\)
\(=\left(a-b\right)\left(a-c\right)\left(b-c\right)\)
12, \(x^3-7x-6\)
\(=x^3-3x^2+3x^2-9x+2x-6\)
\(=x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2+3x+2\right)\)
\(=\left(x-3\right)\left(x^2+x+2x+2\right)\)
\(=\left(x-3\right)\left[x\left(x+1\right)+2\left(x+1\right)\right]\)
\(=\left(x-3\right)\left(x+2\right)\left(x+1\right)\)
13, \(x^4+4\)
\(=x^4+4x^2+4-4x^2\)
\(=\left(x^2+2\right)^2-4x^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
14, \(a^4+64\)
\(=a^4+16a^2+64-16a^2\)
\(=\left(a^2+8\right)^2-16a^2\)
\(=\left(a^2-4a+8\right)\left(a^2+4a+8\right)\)
15, \(x^5+x+1\)
\(=x^5-x^2+x^2+x+1\)
\(=x^2\left(x^3-1\right)+x^2+x+1\)
\(=x^2\left(x-1\right)\left(x^2+x+1\right)+x^2+x+1\)
\(=\left(x^2+x+1\right)\left[x^2\left(x-1\right)+1\right]\)
16, \(x^5+x-1\)
\(=x^5-x^4+x^3+x^4-x^3+x^2-x^2+x-1\)
\(=x^3\left(x^2-x+1\right)-x^2\left(x^2-x+1\right)-\left(x^2-x+1\right)\)
\(=\left(x^2-x+1\right)\left(x^3-x^2-1\right)\)
17, \(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
\(=\left(x^2+x\right)\left(x^2+x-2\right)-15\)
19, \(\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\) (*)
Đặt \(x^2+8x+7=a\) ta có:
(*) \(\Leftrightarrow a\left(a+8\right)+15\)
\(\Leftrightarrow a^2+8a+15\)
\(\Leftrightarrow a^2+3a+5a+15\)
\(\Leftrightarrow a\left(a+3\right)+5\left(a+3\right)\)
\(\Leftrightarrow\left(a+3\right)\left(a+5\right)\)
Trả lại biến cũ ta có: (*) \(\Leftrightarrow\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)
20, \(\left(x^2+3x+1\right)\left(x^2+3x+2\right)-6\) (*)
Đặt \(x^2+3x+1=a\) ta có:
(*) \(\Leftrightarrow a\left(a+1\right)-6\)
\(\Leftrightarrow a^2+a-6\)
\(\Leftrightarrow a^2+3a-2a-6\)
\(\Leftrightarrow a\left(a+3\right)-2\left(a+3\right)\)
\(\Leftrightarrow\left(a-2\right)\left(a+3\right)\)
Trả lại biến cũ ta có: (*) \(\Leftrightarrow\left(x^2+3x-1\right)\left(x^2+3x+5\right)\)

Bài 1:
a) 25x2 - 10xy + y2 = (5x - y)2
b) 81x2 - 64y2 = (9x)2 - (8y)2 = (9x - 8y)(9x + 8y)
c) 8x3 + 36x2y + 54xy2 + 27y3
= 8x3 + 27y3 + 36x2y + 54xy2
= (2x + 3y)(4x2 - 6xy + 9y2) + 18xy(2x + 3y)
= (2x + 3y)(4x2 - 6xy + 18xy + 9y2)
= (2x + 3y)(4x2 + 12xy + 9y2)
= (2x + 3y)(2x + 3y)2 = (2x + 3y)3
c) (a2 + b2 - 5)2 - 4(ab + 2)2 = (a2 + b2 - 5)2 - 22(ab + 2)2
= (a2 + b2 - 5)2 - (2ab + 4)2
= (a2 + b2 - 5 - 2ab - 4)(a2 + b2 - 5 + 2ab + 4)
= (a2 - 2ab + b2 - 9)(a2 + 2ab + b2 - 1)
= \(\left [ (a - b)^{2} - 3^{2} \right ]\)\(\left [ (a + b)^{2} - 1\right ]\)
= (a - b - 3)(a - b + 3)(a + b - 1)(a + b + 1)
pn đăng mỗi lần vài bài thôi chứ đăng nhìn ngán lắm
Bài 2:
a) 2x3 + 3x2 + 2x + 3
= 2x3 + 2x + 3x2 + 3
= 2x(x2 + 1) + 3(x2 + 1)
= (x2 + 1)(2x + 3)
b)x3z + x2yz - x2z2 - xyz2
= xz(x2 + xy - xz - yz)
= \(xz\left [ x(x + y) - z(x + y) \right ]\)
= xz(x + y)(x - z)
c) x2y + xy2 - x - y
= xy(x + y) - (x + y)
= (x + y)(xy - 1)
d) 8xy3 - 5xyz - 24y2 + 15z
= 8xy3 - 24y2 - 5xyz + 15z
= 8y2(xy - 3) - 5z(xy - 3)
= (xy - 3)(8y2 - 5z)
e) x3 + y(1 - 3x2) + x(3y2 - 1) - y3
= x3 - y3 + y - 3x2y + 3xy2 - x
= (x - y)(x2 + xy + y2) - 3xy(x - y) - (x - y)
= (x - y)(x2 + xy + y2 - 3xy - 1)
= (x - y)(x2 - 2xy + y2 - 1)
= \((x - y)\left [ (x - y)^{2} - 1 \right ]\)
= (x - y)(x - y - 1)(x - y + 1)
câu f tương tự

bài 1.
a) (4x3 - 2)(2x3- x + \(\dfrac{5}{8}\))
= 8x6 - 4x4 + \(\dfrac{5}{2}\)x3 - 4x3 + 2x - \(\dfrac{5}{4}\)
b) (x2y2 - xy + y)(x - y)
= x3y2 - x2y + xy - x2y3 + xy2 - y2
c) (x + 2y)(x2 - 2xy + y2)
= x3 + 8y3
d) (7x - 3)(7x + 3) + (2x - 3)2
= 49x2 - 9 + 4x2 - 12x + 9
= 53x2 - 12x
Bài 2.
a) 4(3x - 1) - 2(5 - 3x) = 24
12x - 4 - 10 + 6x - 24 = 0
18x - 38 = 0
\(\Rightarrow\) 18x = 38
\(\Rightarrow\) x = \(\dfrac{19}{9}\)
b) 4x2 - 9 = 0
\(\Rightarrow\) 4x2 = 9
\(\Rightarrow\) x2 = \(\dfrac{9}{4}\)
\(\Rightarrow\) x = \(\pm\dfrac{3}{2}\)
vậy x = 3/2 hoặc x = -3/2
c) x3 - 25x = 0
x(x2 - 25) = 0
x(x - 5)(x + 5) = 0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-5=0\\x+5=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
d) (x2 + 4)2 - 16x2 = 0
(x2 + 4 - 4x)(x2 + 4 + 4x) = 0
\(\Rightarrow\) (x - 2)2.(x + 2)2 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=0\\\left(x+2\right)^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Bài 3.
a) x(x + y) + y(x + y)
Ta có:
x(x + y) + y(x + y)
= (x + y)(x + y)
= (x + y)2
Thay x = 2004 và y = -2003 vào biểu thức đại số ta có:
[2004 + (-2003)]2 = 12
= 1
b) x2 + xy - xz - yz
Ta có:
x2 + xy - xz - yz
= (x2 + xy) - (xz + yz)
= x(x + y) - z(x + y)
= (x - z)(x + y)
Thay x= 6,5; y = 3,5 và z = 37,5 vào biểu thức đại số, ta có:
(6,5 - 37,5)(6,5 + 3,5)
= -31 . 10
= -310
c) x2 - 6xy + 9y2
ta có:
x2 - 6xy + 9y2
= (x - 3y)2
Thay x = 14 và y = -2 vào biểu thức đại số, ta có:
[14 - (-2)]2 = (14 + 2)2
= 162 = 256
Nhớ tik mik nhé không lần sau mik ko giúp đâu ![]()
![]()
![]()
có j ko hỉu cứ bình luận ở dưới![]()
![]()
![]()

Bài 1 : Ta có :
x^3-x^2-7x-a x-3 x^2 x^3-3x^2 2x^2-7x-a + 2x 2x^2 -6x -x - a - 1 -x + 3
Để \(x^3-x^2-7x-a\) chia hết cho x-3 thì :
-x - a = - x + 3
<=> -x + x - a = 3
<=> a = - 3
Vậy GT của a là - 3
Bài 2 :
a) \(x^2-2xy-9z^2+y^2\)
= \(\left(x^2-2xy+y^2\right)-9z^2\)
= \(\left(x-y\right)^2-\left(3z\right)^2\)
= \(\left(x-y-3z\right)\left(x-y+3z\right)\) (1)
Thay x = 6 ; y=-4 ; z= 30 vào BT (1) ta được :
\(\left(x-y-3z\right)\left(x-y+3z\right)=\left(6+4-3.30\right)\left(6+4+3.30\right)\) = (-80) .100 = -8000
Vậy tại x = 6 ; y=-4 ; z=30 thì GT của BT (1) là -8000
b) \(\left(x^3-y^3\right):\left(x^2+xy+y^2\right)\)
= \(\left(x-y\right)\left(x^2+xy+y^2\right):\left(x^2+xy+y^2\right)\)
= ( x- y ) (2)
Thay x = \(\dfrac{2}{3}v\text{à}\) y = \(\dfrac{1}{3}\) vào biểu thức (2) ta được :
\(\left(x-y\right)=\left(\dfrac{2}{3}-\dfrac{1}{3}\right)=\dfrac{1}{3}\)
Vậy tại x = \(\dfrac{2}{3}v\text{à}\) y = \(\dfrac{1}{3}\) thì GT của BT (2) là \(\dfrac{1}{3}\)
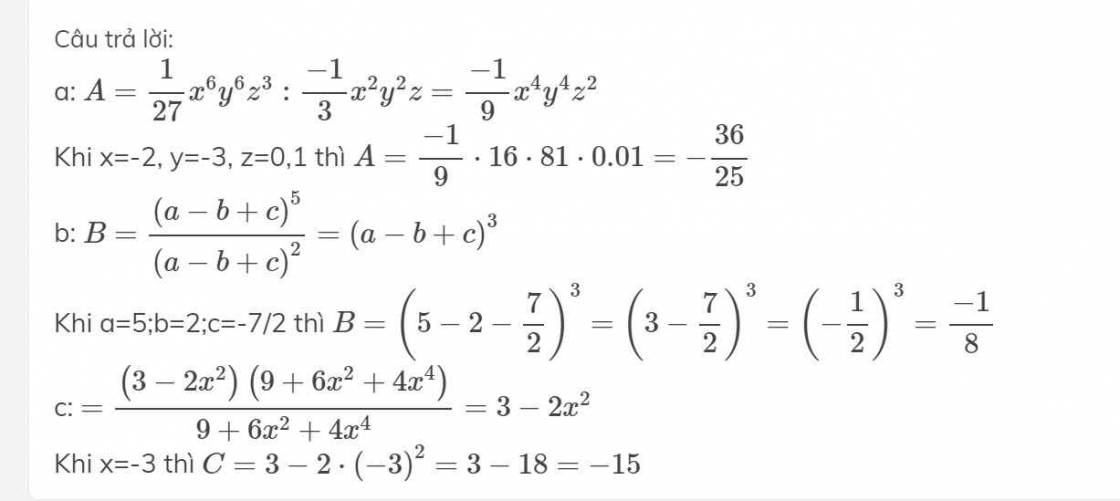



a: \(A=\dfrac{1}{27}x^6y^6z^3:\dfrac{-1}{3}x^2y^2z=\dfrac{-1}{9}x^4y^4z^2\)
Khi x=-2, y=-3, z=0,1 thì \(A=\dfrac{-1}{9}\cdot16\cdot81\cdot0.01=-\dfrac{36}{25}\)
b: \(B=\dfrac{\left(a-b+c\right)^5}{\left(a-b+c\right)^2}=\left(a-b+c\right)^3\)
Khi a=5;b=2;c=-7/2 thì \(B=\left(5-2-\dfrac{7}{2}\right)^3=\left(3-\dfrac{7}{2}\right)^3=\left(-\dfrac{1}{2}\right)^3=\dfrac{-1}{8}\)
c: \(=\dfrac{\left(3-2x^2\right)\left(9+6x^2+4x^4\right)}{9+6x^2+4x^4}=3-2x^2\)
Khi x=-3 thì \(C=3-2\cdot\left(-3\right)^2=3-18=-15\)