Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không có khái niệm hàm số đơn điệu tại 1 điểm x hoặc y nào đó, nên bạn xem lại đề

\(g'\left(x\right)=\left(2x-8\right)f'\left(x^2-8x+m\right)\)
Ta không cần quan tâm tới nhân tử \(\left(x-1\right)^2\) ở \(f'\left(x\right)\) vì đó là biểu thức mũ chẵn nên ko làm \(f'\left(x\right)\) đổi dấu khi đi qua \(x=1\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}2x-8=0\Rightarrow x=4\\\left(x^2-8x+m\right)^2-2\left(x^2-8x+m\right)=0\left(1\right)\end{matrix}\right.\)
Để hàm số đồng biến trên \(\left(4;+\infty\right)\Rightarrow\left(1\right)\) vô nghiệm hoặc tất cả các nghiệm của (1) đều không lớn hơn 4
\(\left(1\right)\Leftrightarrow\left(x^2-8x+m\right)\left(x^2-8x+m-2\right)=0\)
TH1: \(16-m+2\le0\Rightarrow m\ge18\)
TH2: Nhận thấy 2 pt \(\left\{{}\begin{matrix}x^2-8x+m=0\\x^2-8m+m-2=0\end{matrix}\right.\)
Đều có trung bình cộng hai nghiệm \(\frac{x_1+x_2}{2}=4\Rightarrow\) nếu 2 pt này có nghiệm thì luôn có ít nhất 1 nghiệm lớn hơn 4 \(\Rightarrow\) ko thỏa mãn
Vậy \(m\ge18\) \(\Rightarrow\) có \(99-18+1=82\) giá trị nguyên của m

\(g'\left(x\right)=-f'\left(3-x\right)=\left(x-3\right)\left(2-x\right)^2\left(\left(3-x\right)^2+9\left(3-x\right)+9\right)\)
Không cần quan tâm tới \(\left(2-x\right)^2\) do \(g'\left(x\right)\) ko đổi dấu khi đi qua điểm dừng này
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\\left(3-x\right)^2+m\left(3-x\right)+9=0\left(1\right)\end{matrix}\right.\)
Để \(g\left(x\right)\) đồng biến trên \(\left(3;+\infty\right)\Rightarrow\left(1\right)\) vô nghiệm hoặc các nghiệm của (1) đều không lớn hơn 3
\(\left(1\right)\Leftrightarrow h\left(x\right)=x^2-\left(m+6\right)x+3m+18=0\)
\(\Delta=m^2-36\)
TH1: \(\Delta< 0\Rightarrow m^2-36< 0\Rightarrow-6< m< 6\)
TH2: \(\left\{{}\begin{matrix}\Delta\ge0\\h\left(3\right)>0\\\frac{m+6}{2}< 3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge6\\m\le-6\end{matrix}\right.\\9>0\\m< 0\end{matrix}\right.\) \(\Rightarrow m\le-6\)
Vậy \(m< 6\) thì \(g\left(x\right)\) đồng biến trên \(\left(3;+\infty\right)\Rightarrow\) có 5 giá trị nguyên dương

Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng

Lời giải:
Ta có \(4^x-2m.2^x+(2m^2+5)=0\)
Coi \(2^x=a\) thì pt chuyển về pt bậc 2:
\(a^2-2ma+(2m^2+5)=0(*)\)
Ta thấy \(\Delta'=m^2-(2m^2+5)=-(m^2+5)<0\), do đó pt $(*)$ vô nghiệm, tức là không tồn tại $a$, kéo theo không tồn tại $x$
Do đó không tồn tại giá trị nào của $m$ thỏa mãn đkđb

a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc
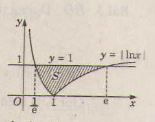
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
\(I=\int e^xcosxdx\Rightarrow\left\{{}\begin{matrix}u=cosx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-sinx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=e^xcosx+\int e^xsinx.dx=e^xcosx+I_1\)
\(I_1=\int e^xsinx\Rightarrow\left\{{}\begin{matrix}u=sinx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=cosx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I_1=e^xsinx-\int e^xcosx.dx=e^x.sinx-I\)
\(\Rightarrow I=e^xcosx+e^xsinx-I\Rightarrow2I=e^x\left(cosx+sinx\right)\)
\(\Rightarrow I=e^x\left(\frac{1}{2}cosx+\frac{1}{2}sinx\right)+C\Rightarrow\left\{{}\begin{matrix}A=\frac{1}{2}\\B=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow A+B=1\)