Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (2 điểm)
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật: (0,5 điểm)
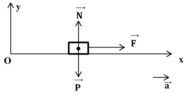
+ Viết phương trình định luật II Niu-tơn: 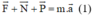 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (1) lên trục Ox ta được: F = m.a (0,5 điểm)
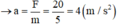 (0,5 điểm)
(0,5 điểm)
b) (2 điểm)
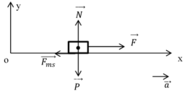
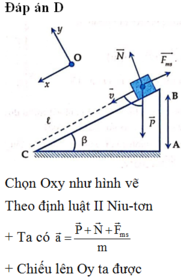
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật
+ Viết phương trình định luật II Niu-tơn
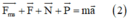 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (2) lên trục Oy: N – P = 0
→ N = P = m.g = 5.10 = 50N (0,5 điểm)
+ Độ lớn lực ma sát: F m s = μ.N = 0,2.50 = 10N (0,5 điểm)
+ Chiếu pt (2) lên trục Ox: F – F m s = ma
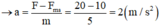 (0,5 điểm)
(0,5 điểm)


Công của lực ma sát khi vật chuyển động được nửa đoạn đường trên mặt phẳng nghiêng là
![]()

200g=0,2kg
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

Lực ma sát tác dụng lên vật có độ lớn bằng công thức:
Quãng đường vật trượt đến khi dừng là:
Công của lực ma sát đã thực hiện đến khi vật dừng lại là
Ta có : \(F_{ms}=N.\mu=mg\mu=100u\left(N\right)\)
Lại có : \(v^2-v^2_0=2as\)
\(\Rightarrow2as=0^2-3^2=-9\)
\(\Rightarrow S=-\dfrac{9}{2a}\)
Mà \(F_{ms}=ma\)
\(\Rightarrow a=\dfrac{-F}{m}=\dfrac{-100u}{10}=-10u\left(\dfrac{m}{s^2}\right)\) ( \(\overrightarrow{a}\uparrow\downarrow\overrightarrow{F}\) )
\(\Rightarrow S=-\dfrac{9}{-2.10u}=\dfrac{9}{20u}\left(m\right)\)
Ta có : \(A=F_{ms}.s.cos180=\dfrac{\left(-1\right).9}{20u}.100u=-45\left(J\right)\)
Vậy ...

Câu trả lời đúng là A. Fmst = μmg. Biểu thức này xác định lực ma sát trượt là tích của hệ số ma sát trượt μ, khối lượng vật m và gia tốc trọng trường g.

Tóm tắt: \(m=2\)tấn=2000kg;\(\mu=0,06;g=10\)m/s2
\(F_{ms}=?\)
Bài giải:
Áp lực do xe tác dụng lên mặt đường bằng trọng lực của xe:
\(\Rightarrow N=P=mg=10\cdot2\cdot1000=20000N\)
Ta có: \(F_{ms}=\mu\cdot N\)
\(=0,06\cdot20000=1200N\)

tham khảo sai rồi, bài này chỉ áp dụng công thức thôi, không cho mặt phẳng nghiêng góc bao nhiêu độ nên làm đơn giản nhé.
Độ lớn lực ma sát trượt:
\(F_{mst}=\mu mg=0,5\cdot5\cdot10=25N\)