Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: SABCD = 828m2
⇔ AD.AB = 828
Mà AB = 23m ⇒ AD = 36m.
Diện tích hình thang ABED là:
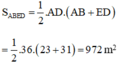

Hình vẽ thế này đúng ko:
A B D E C 23 cm 31 cm
Ta có: \(S_{ABCD}=AB.AD=828m^2\)
Nên \(AD=\frac{828}{23}=36\left(m\right)\)
Do đó diện tích của hình thang ABED là:
\(S_{ABED}=\frac{\left(AB+DE\right).AD}{2}=\frac{\left(23+31\right).36}{2}=972\left(m^2\right)\)

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.


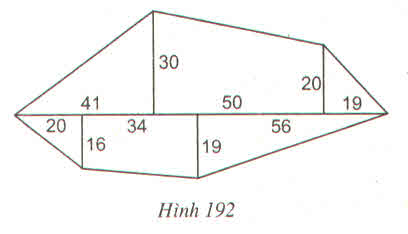
S1=\(\dfrac{30.41}{2}=615\left(cm^2\right)\)
S2=\(\dfrac{\left(30+20\right).50}{2}=1250\left(cm^2\right)\)
S3=\(\dfrac{19.20}{2}=190\left(cm^2\right)\)
S4=\(\dfrac{19.56}{2}=532\left(cm^2\right)\)
S5=\(\dfrac{\left(19+16\right).34}{2}=595\left(cm^2\right)\)
S6=\(\dfrac{16.20}{2}=160\left(cm^2\right)\)
=> S= S1 + S2 +S3 +S4 +S5 +S6= 615+1250+190+532+595+160=3342(m2)

A B C D E F H G L M N P
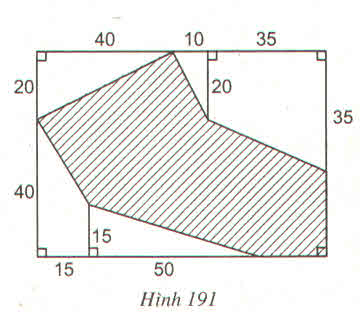
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.

Ta có:
SABCD=(40+10+35).(20+40) = 5100 (cm2)
S1=\(\dfrac{40.20}{2}=400\left(cm^2\right)\)
S2=\(\dfrac{10.20}{2}=100\left(cm^2\right)\)
S3=\(\dfrac{\left(20+35\right).35}{2}=962,5\left(cm^2\right)\)
S4=\(\dfrac{50.15}{2}=375\left(cm^2\right)\)
S5=\(\dfrac{\left(15+40\right).15}{2}=412,5\left(cm^2\right)\)
=> Shình gạch sọc= S - ( S1+S2+S3+S4+S5)= 5100-(400+100+962,5+375+412,5)=2850(cm2)

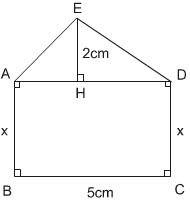
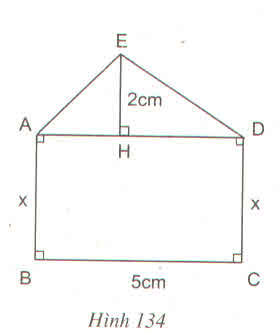
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm

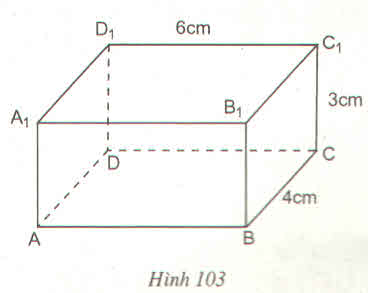
\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)
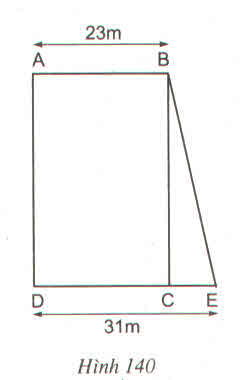
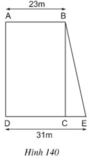





Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)