Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách 1: y' = (9 -2x)'(2x3- 9x2 +1) +(9 -2x)(2x3- 9x2 +1)' = -2(2x3- 9x2 +1) +(9 -2x)(6x2 -18x) = -16x3 +108x2 -162x -2.
Cách 2: y = -4x4 +36x3 -81x2 -2x +9, do đó
y' = -16x3 +108x2 -162x -2.
b) y' = .(7x -3) +
(7x -3)'=
(7x -3) +7
.
c) y' = (x -2)'√(x2 +1) + (x -2)(√x2 +1)' = √(x2 +1) + (x -2) = √(x2 +1) + (x -2)
= √(x2 +1) +
=
.
d) y' = 2tanx.(tanx)' - (x2)' =
.
e) y' = sin
=
sin
.

1: ĐKXĐ: \(\cos^2x>=1\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x>=1\\\cos x< =-1\end{matrix}\right.\Leftrightarrow x\in\left\{k2\Pi;\Pi+k2\Pi\right\}\)
2: ĐKXĐ: \(1-\sin2x>0\)
\(\Leftrightarrow\sin2x< 1\)
\(\Leftrightarrow2x< \dfrac{\Pi}{2}+k\Pi\)
hay \(x< \dfrac{\Pi}{4}+\dfrac{k\Pi}{2}\)

1.
\(\lim\limits_{x\to (-1)-}\frac{\sqrt{x^2-3x-4}}{1-x^2}=\lim\limits_{x\to (-1)-}\frac{\sqrt{(x+1)(x-4)}}{(1-x)(1+x)}\)
\(=\lim\limits_{x\to (-1)-}\frac{\sqrt{4-x}}{(x-1)\sqrt{-(x+1)}}=-\infty\) do:
\(\lim\limits_{x\to (-1)-}\frac{\sqrt{4-x}}{x-1}=\frac{-\sqrt{5}}{2}<0\) và \(\lim\limits_{x\to (-1)-}\frac{1}{\sqrt{-(x+1)}}=+\infty\)
2.
\(\lim\limits_{x\to 2+}\left(\frac{1}{x-2}-\frac{x+1}{\sqrt{x+2}-2}\right)=\lim\limits_{x\to 2+}\frac{1-(x+1)(\sqrt{x+2}+2)}{x-2}=-\infty\) do:
\(\lim\limits_{x\to 2+}\frac{1}{x-2}=+\infty\) và \(\lim\limits_{x\to 2+}[1-(x+1)(\sqrt{x+2}+2)]=-11<0\)

Lời giải:
a) y' = =
, y" =
=
=
.
b) y' = =
;
y" = =
=
.
c) y' = ; y" =
=
=
.
d) y' = 2cosx.(cosx)' = 2cosx.(-sinx) = - 2sinx.cosx = -sin2x,
y" = -(2x)'.cos2x = -2cos2x.
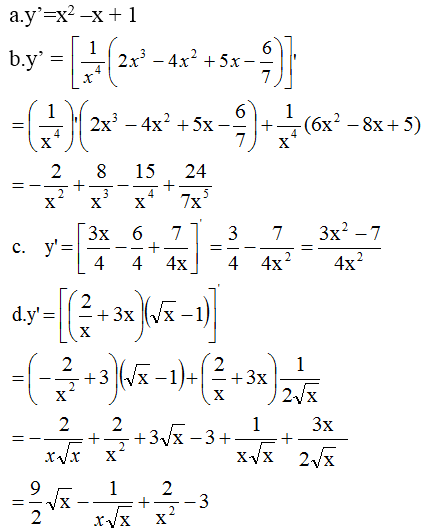
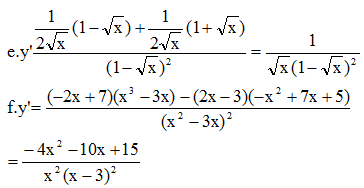
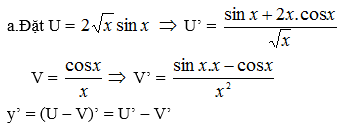
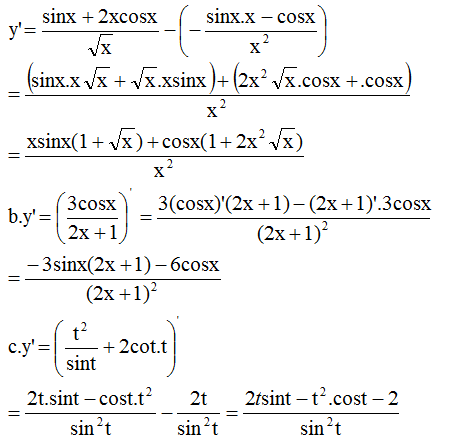
1/ \(y'=\left(1-3x\right)'\sqrt{x-3}+\left(1-3x\right)\left(\sqrt{x-3}\right)'=-3\sqrt{x-3}+\dfrac{1}{2\sqrt{x-3}}\left(1-3x\right)\)
2/ \(y'=\dfrac{1}{\sqrt{2x+1}}-\dfrac{1}{\left(x+1\right)^2}\)
3/ \(y'=\dfrac{1}{2}.\sqrt{\dfrac{1+x}{1-x}}.\left(\dfrac{1-x}{1+x}\right)'=\dfrac{1}{2}\sqrt{\dfrac{1+x}{1-x}}.\dfrac{-2}{\left(1+x\right)^2}=-\sqrt{\dfrac{1+x}{1-x}}.\dfrac{1}{\left(1+x\right)^2}\)
4/ \(y'=\left(\cos5x\right)'.\cos7x+\cos5x.\left(\cos7x\right)'=-5\sin5x.\cos7x-7\cos5x\sin7x\)
5/ \(y'=\left(\cos x\right)'\sin^2x+\cos x\left(\sin^2x\right)'=-\sin^3x+2\sin x.\cos^2x\)
6/ \(y'=\left(\tan^42x\right)'=4.\tan^32x.\dfrac{2}{\cos^22x}\)
7/ \(y'=\dfrac{2\sin x+2\cos x-2x.\cos x+2x\sin x}{\left(\sin x+\cos x\right)^2}\)
Ờm, bạn tự rút gọn nhé :) Mình đang hơi lười :b