QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
K
5 tháng 8 2020
Ta có \(y'=x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a\)
Để y có cực đại và cực tiểu thì y' đổi dấu hai lần, tức là:
\(\Delta=\left(sina+cosa\right)^2-3sin2a>0\)
\(\Leftrightarrow1+sin2a-3sin2a>0\)
\(\Leftrightarrow sin2a< \frac{1}{2}\)
\(\Leftrightarrow\frac{5\eta}{6}+k2\eta< 2a< \frac{13\eta}{6}+k2\eta\)
\(\Leftrightarrow\frac{5\eta}{12}+k\eta< a< \frac{13\eta}{12}+k\eta\)
K
5 tháng 8 2020
Tại cực trị \(y'=0\Leftrightarrow x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a=0\)(*)
(*) cho ta\(x_1+x_2=sina+cosa,x_1x_2=\frac{3}{4}sin2a\)(*)
Để \(x_1+x_2=x^2_1+x^2_2\)thì \(x_1+x_2=\left(x_1+x_2\right)^2-2x_1+x_2\)
\(\Leftrightarrow sina+cosa=\left(sina+cosa\right)^2-\frac{3}{2}sin2a\)
\(\Leftrightarrow sina+cosa=1-\frac{1}{2}sin2a\)
Đặt \(t=cosa+sina=\sqrt{2}cos\left(a-\frac{\eta}{4}\right),t\in\left[-\sqrt{2},\sqrt{2}\right]\)
\(t^2=1+sin2a\Rightarrow sin2a=t^2-1\)
Do đó phương trình trên trở thành:
\(t=1-\frac{1}{2}\left(t^2-1\right)\Leftrightarrow2t=3-t^2\)
\(\Leftrightarrow t^2+2t-3=0\Leftrightarrow t=1,t=-3\)
Vì\(t\in\left[-\sqrt{2},\sqrt{2}\right]\)nên chỉ nhân t=1
\(\Rightarrow cos\left(a-\frac{\eta}{4}\right)=\frac{\sqrt{2}}{2}=cos\frac{\eta}{4}\)
\(\Leftrightarrow a-\frac{\eta}{4}=\pm\frac{\eta}{4}+k2\eta\)
\(\Leftrightarrow a=k2\eta\)hay \(a=\frac{\eta}{2}+k2\eta\)(thỏa điều kiện câu a)
CM
17 tháng 8 2019
Chọn A
Áp dụng sin u / , với u = cos 2 x tan 2 x
y ' = cos cos 2 x . tan 2 x . cos 2 x . tan 2 x / .
Tính cos 2 x . tan 2 x / , bước đầu sử dụng u . v / , sau đó sử dụng u α / .
cos 2 x . tan 2 x / = cos 2 x / . tan 2 x + tan 2 x / . cos 2 x
= 2 cos x cos x / tan 2 x + 2 tan x tan x / cos 2 x
= − 2 sin x cos x tan 2 x + 2 tan x 1 cos 2 x cos 2 x = − sin 2 x tan 2 x + 2 tan x .
Vậy y ' = cos cos 2 x . tan 2 x − sin 2 x tan 2 x + 2 tan x
CM
29 tháng 1 2018
Chọn C
Đầu tiên áp dụng u α / , với u = sin cos tan 4 3 x
y ' = 2 sin cos tan 4 3 x . sin cos tan 4 3 x /
Sau đó áp dụng sin u / , với u = cos tan 4 3 x
y ' = 2 sin cos tan 4 3 x . cos cos tan 4 3 x . cos tan 4 3 x /
Áp dụng cos u / , với u = tan 4 3 x .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x . tan 4 3 x / .
Áp dụng u α / , với u = tan 3 x
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . tan 3 x / .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 2 3 x . 3 x / .
y ' = − sin 2 cos tan 4 3 x . sin tan 4 3 x .4 tan 3 3 x . 1 + tan 3 3 x .3
5 tháng 5 2016
xét hàm số y=\(x.e^x.lnx\)
Ta có y' =\(e^xlnx+xe^xlnx+xe^x.\frac{1}{x}\)
=\(e^xlnx+xe^xlnx+e^x\left(1+lnx+x.lnx\right)\)
CM
27 tháng 4 2017
Chọn D
Bước đầu tiên áp dung công thức u α / với u = sin 2 x + 1
Vậy
y ' = sin 3 2 x + 1 / = 3 sin 2 2 x + 1 . sin 2 x + 1 / .
* Tính sin 2 x + 1 / : Áp dụng sin u / , với u = 2 x + 1
Ta được:
sin 2 x + 1 / = cos 2 x + 1 . 2 x + 1 / = 2 cos 2 x + 1 .
⇒ y ' = 3. sin 2 2 x + 1 .2 cos 2 x + 1 = 6 sin 2 2 x + 1 cos 2 x + 1 .
CM
26 tháng 12 2018
Chọn D.
Bước đầu tiên ta áp dụng công thức u α / với u = sin x 1 + cos x
y ' = 3 sin x 1 + cos x 2 . sin 1 + cos x /
Tính :
sin x 1 + cos x / = sin x / 1 + cos x − 1 + cos x / . sin x 1 + cos x 2 = cos x 1 + cos x + sin 2 x 1 + cos x 2
= cos x + cos 2 x + sin 2 x 1 + cos x 2 = cosx + 1 ( 1 + c osx) 2 = 1 1 + cos x .
Vậy
y ' = 3 sin x 1 + cos x 2 . 1 1 + cos x = 3 sin 2 x 1 + cos x 3
CM
23 tháng 1 2019
y = tan x + cot x ⇒ y ' = ( tan x + cot x ) ' = ( tan x ) ' + ( cot x ) ' = 1 cos 2 x − 1 sin 2 x
Chọn đáp án D
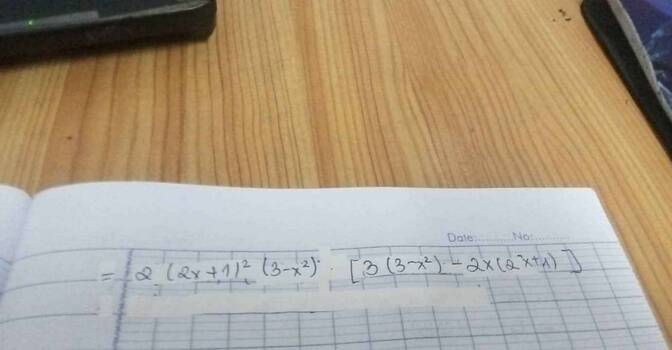
y'=( xsina+ cosa )'( xcosa - sina)+( xsina+ cosa )( xcosa - sina)'
=(cosx-sinx)( xcosa - sina)+( xsina+ cosa )(-sinx-cosa);
=cosx.xcosa-sinx.sina-xsina.sinx-cosa.xsina-cosa.sinx-cos²a