Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Chiều dài của thanh: \(l=l_0(1+\alpha.\Delta t)\)
Thanh nhôm: \(l=50.[1+24.10^{-6}.(170-20)]=50,18cm\)
Thanh thép: \(l=50,12.[1+12.10^{-6}.(170-20)]=50,21cm\)
b/ Giả sử ở nhiệt độ t, hai thanh có cùng chiều dài
\(\Rightarrow 50.[1+24.10^{-6}.(t-20)]=50,12.[1+12.10^{-6}.(t-20)]\)
Bạn giải phương trình trên rồi tìm t nhé ![]()

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
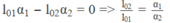
hay:
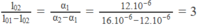
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l 1 - l 2 l 1 = l 01 α 1 t - l 02 α 2 t = ( l 01 α 1 - l 02 α 2 )t = 25 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t.
Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
l 01 α 1 - l 02 α 2 = 0 ⇒ l 02 / l 01 = α 1 / α 2
hay:
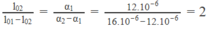
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 2( l 01 - l 02 ) = ∆ l = 2.25 = 50 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 50 + 25 = 75 mm.

Bài 1: bất kì nhiệt độ nào thì độ dài thép > độ dài đồng 5cm nên không có nhiệt độ
lo thép - lo đồng =5 <=> lo thép = 5 + lo đồng
Ta có
l thép - l đồng = 5
<=> lo thép (1 + 12.10^6) - lo đồng(1 + 16.10^-6) = 5
<=> (5 + lo đồng) (1+12.10^6) - lo đồng(1+16.10^6) = 5
=> lo đồng = 15 cm
lo thép = 5 + lo đồng = 5 + 15 = 20 cm
Bài 2:
Ở t=1000C=1000C, chiều dài của thanh sắt \(l_1=l_0\left(1+\alpha_1\Delta t\right)\) ; chiều dài của thanh kẽm :
l2=\(l_0\left(1+\alpha_2\Delta t\right)\)
Vì α2>α1 nên l2−l1=1mm
⇔l0(α0−α1)t=1⇒l0=442,5(mm)⇔l0(α2−α1)t=1⇒l0=442,5(mm).

Đáp án: D
Gọi l1 là chiều dài của thanh đồng thau, l2 là chiều dài của thanh thép.
Theo giả thiết, ở nhiệt độ bất kỳ ta đều có:
l2 – l1 = 2 cm (1)
Ở 0 oC ta cũng có:
l02 – l01 = 2 cm (2)
Mặt khác, ta lại có:
l2 = l02(1 + α2∆t) và l1 = l01(1 + α1∆t)
Thay l1, l2 vào (1) ta được:
l02(1 + α2∆t) - l01(1 + α1∆t) = l02 – l01
→ l02.α2 = l01.α1 (3)
Từ (2) và (3), chú ý rằng :
α2 = 18.10-6 K-1 và α1 = 11.10-6 K-1
Ta suy ra được chiều dài của thanh thép và thanh đồng ở 0 oC là 5,1cm và 3,1cm

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = △lαl1△lαl1+ t1= 4,5.10−312.10−6..12,54,5.10−312.10−6..12,5 + 15
=> tmax = 45o.

* Cách 1 :
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : △l = l0a . △t
→ Độ biến dạng thiên nhiệt độ △t :
△t = \(\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-8}}=0,03.10^3=30^oC\)
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = △t + t = 15oC + 30oC = 45oC
Đáp số 450C
* Cách 2 :
Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o.
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : \(\triangle\)l = l0a . \(\triangle\)t
→ Độ biến dạng thiên nhiệt độ \(\triangle\)t :
\(\triangle t=\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-6}}=0,03.10^3=30\) độ C
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = \(\triangle\)t + t = 15 độ C + 30 độ C = 45 độ C
Đáp số 45 độ C
gọi \(l_{01}:\) là chiều dài ban đầu của thanh đồng
\(l_{02}:\) là chiều dài ban đầu của thanh thép
ở bất kì nhiệt độ nào thanh thép cũng dài hơn đồng 5cm
\(l_{01}+5=l_{02}\) (1)
\(l_1+5=l_2\)
\(\Leftrightarrow l_{01}+\alpha_1.\Delta t.l_{01}+5=l_{02}+\alpha_2.\Delta t.l_{02}\)
\(\Rightarrow\alpha_1.l_{01}=\alpha_2.l_{02}\) (2)
\(\frac{\alpha_1}{\alpha_2}=\)\(\frac{4}{3}\) (3)
từ (1),(2),(3)
\(\Rightarrow l_{01}=15cm;l_{02}=20cm\)