K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 4 2017
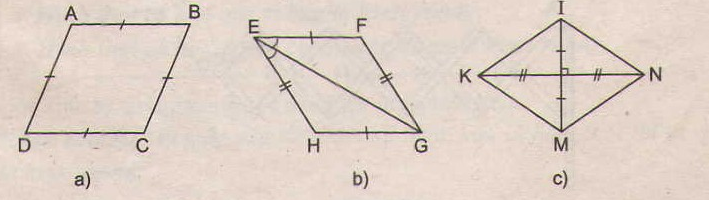
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
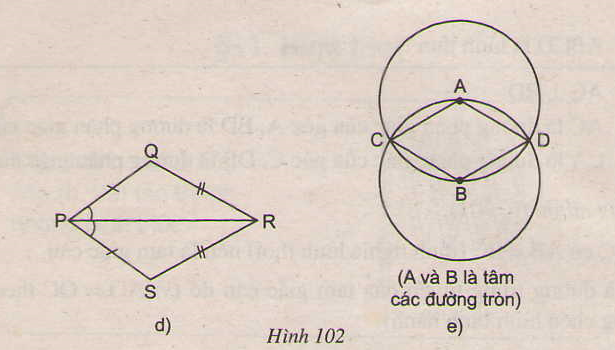
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
21 tháng 4 2017
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
SG
2
21 tháng 4 2017
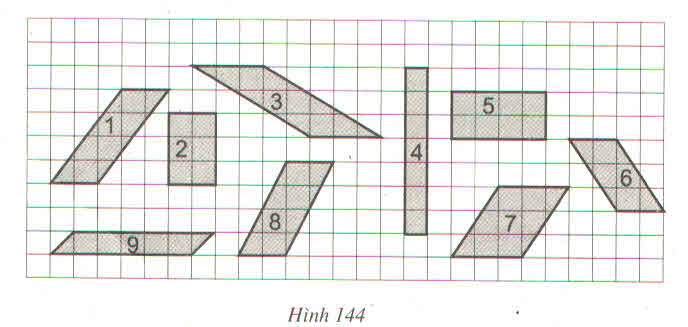
Các hình 2,6,9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3,7 có cùng diện tích là 8 ô vuông.
Hình 4 có diện tích là 7 ô vuông nên không có diện tích với một trong các hình đã cho.
LP
21 tháng 4 2017
Các hình 2, 6, 9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3, 7 có cùng diện tích là 9 ô vuông.
SG
1
22 tháng 4 2017
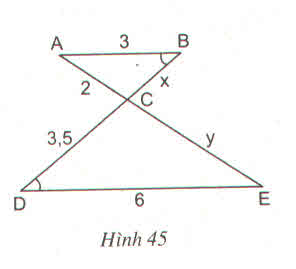
ABDABD^ = ˆBDEBDE^, lại so le trong
=> AB // DE
=> ∆ABC ∽ ∆EDC
=> ABEDABED = BCDCBCDC = ACECACEC
=> 3636 = x3,5x3,5 = 2y2y
=> x = 3.3,563.3,56 = 1.75;
y = 6.236.23 = 4
15 tháng 3 2023
vì góc ADB = góc BDE
=>AB // DE (so le trong)
vì AB//DE nên theo định lí ta - lét ta có :
\(\dfrac{CB}{CE}\) = \(\dfrac{CA}{CD}\)
=>\(\dfrac{x}{y}\) = \(\dfrac{2}{3,5}\) = \(\dfrac{4}{7}\)
vậy chiều dài CB là 4
CE là 7
SG
1
22 tháng 4 2017
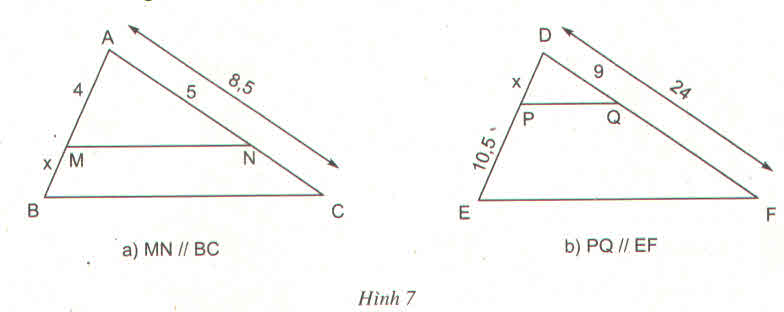
a) MN // BC => BMAMBMAM = CNANCNAN
Mà CN = AN= 8.5 - 5= 3.5
nên x4x4 = 3.553.55 => x = 4.3,554.3,55 = 1,4.
Vậy x = 1,4.
b)
PQ // EF => DPPEDPPE = DQQFDQQF
Mà QF = DF - DQ = 24 - 9 = 15
Nên
x10,5x10,5 = 915915 => x = 10,5.91510,5.915 = 6,3
10 tháng 5 2017
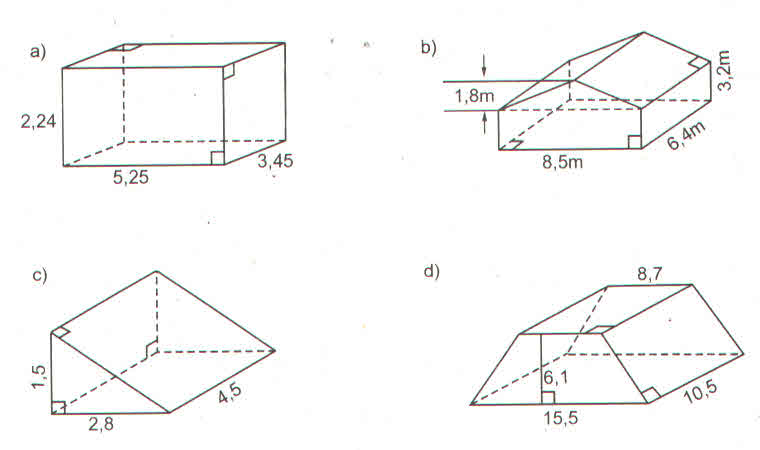
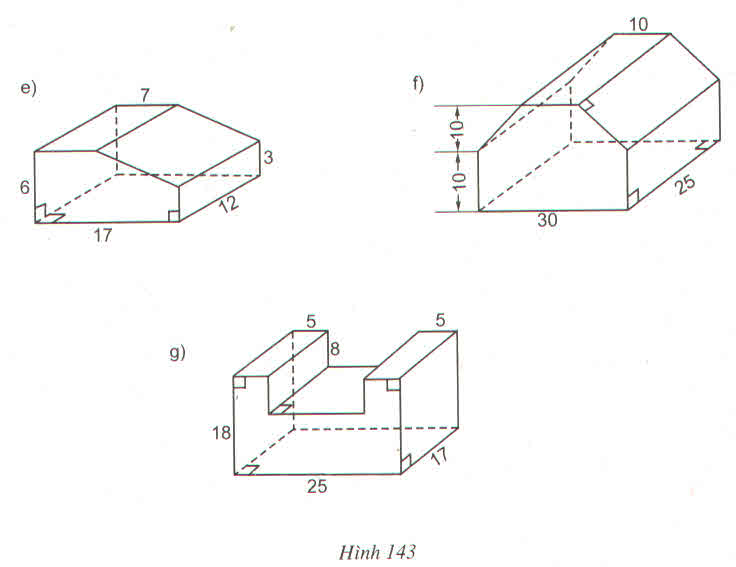
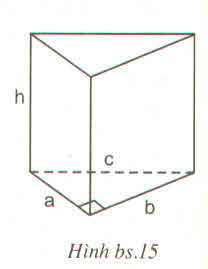
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |
24 tháng 5 2017
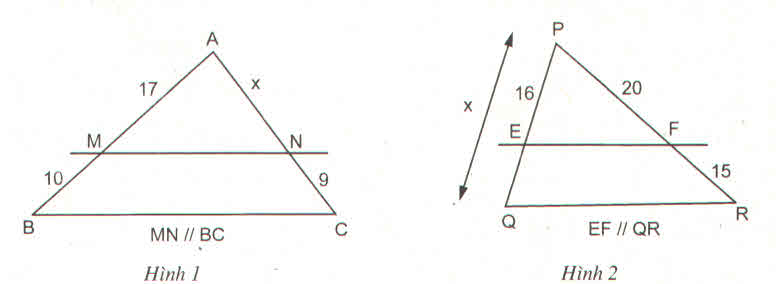
Hình 1
Theo định lý ta lét trong tam giác ta có :
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)=\(\dfrac{17}{27}=\dfrac{x}{x+9}\)=>27x=17x+153
=>x=15.3cm
Hình 2
Theo định lý ta lét trong tam giác ta có :
\(\dfrac{PE}{PQ}=\dfrac{PF}{PR}\)=\(\dfrac{16}{x}=\dfrac{20}{35}\)=>20x=560
=>x=28cm
21 tháng 4 2017
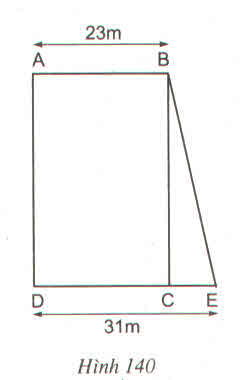
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)
SG
1
H
21 tháng 4 2017
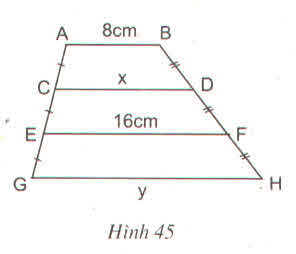
Bài giải:
AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.
Do đó: CD = \(\dfrac{AB+EF}{2}\) = \(\dfrac{8+16}{2}\) = 12
Hay x = 12
Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.
Nên EF = \(\dfrac{CD+GH}{2}\) => GH = 2EF -CD = 2.16 - 12
GH = 20 hay y = 20
Vậy x = 12, y = 20
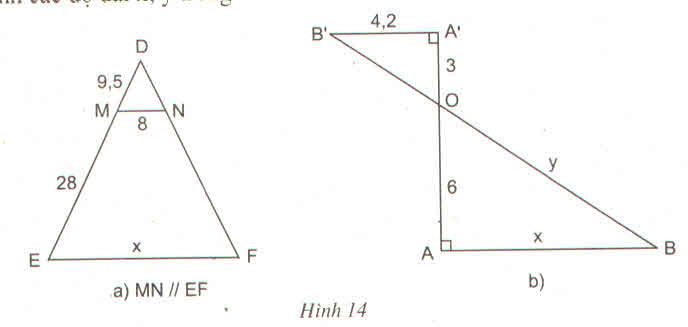
* Trong hình 14a
mà DE = MD + ME = 9.5 + 28 = 37.5
* Trong hình 14b
Ta có A’B’ ⊥ AA'(gt) và AB ⊥ AA'(gt)
=> A’B’ // AB =>
∆ABO vuông tại A
=> OB2 = y2 = OA2 + AB2
=> y2 = 62+ 8,42
=> y2 = 106,56
=> y ≈ 10,3