
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


voi lai phan so sau hon phan so truoc la 2 doi vi anh nhat linh a?

Đặt A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256
=> 2A = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
=> 2A - A = (1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128) - (1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256)
=> A = 1 - 1/256
=> A = 255/256
Vậy: ...




Ta có : \(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)
\(=\frac{49}{5}-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)\)
Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
=> \(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)
=> \(2A-A=1-\frac{1}{32}\Rightarrow A=\frac{31}{32}\)
Vậy \(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)
\(=\frac{49}{5}-\frac{31}{32}=\frac{1413}{160}\)
\(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)\(=\)\(\frac{4189}{480}\)

a. \(\dfrac{17}{13}-\dfrac{14}{23}+\dfrac{9}{13}-\dfrac{9}{23}=\left(\dfrac{17}{13}+\dfrac{9}{13}\right)-\left(\dfrac{14}{23}+\dfrac{9}{23}\right)=\dfrac{26}{13}-\dfrac{23}{23}=2-1=1\)
b.\(\dfrac{49}{5}-\dfrac{1}{2}-\dfrac{1}{4}-\dfrac{1}{32}-\dfrac{1}{16}-\dfrac{1}{32}=\dfrac{49}{5}-\left(1-\dfrac{1}{32}\right)=\dfrac{44}{5}+\dfrac{1}{32}=\dfrac{1413}{160}\)

\(=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{4}{5}+\dfrac{2}{3}+\dfrac{1}{4}\)
=(1/3+2/3)+(1/4+1/4)+(1/5+4/5)
=1+1+1/2
=5/2

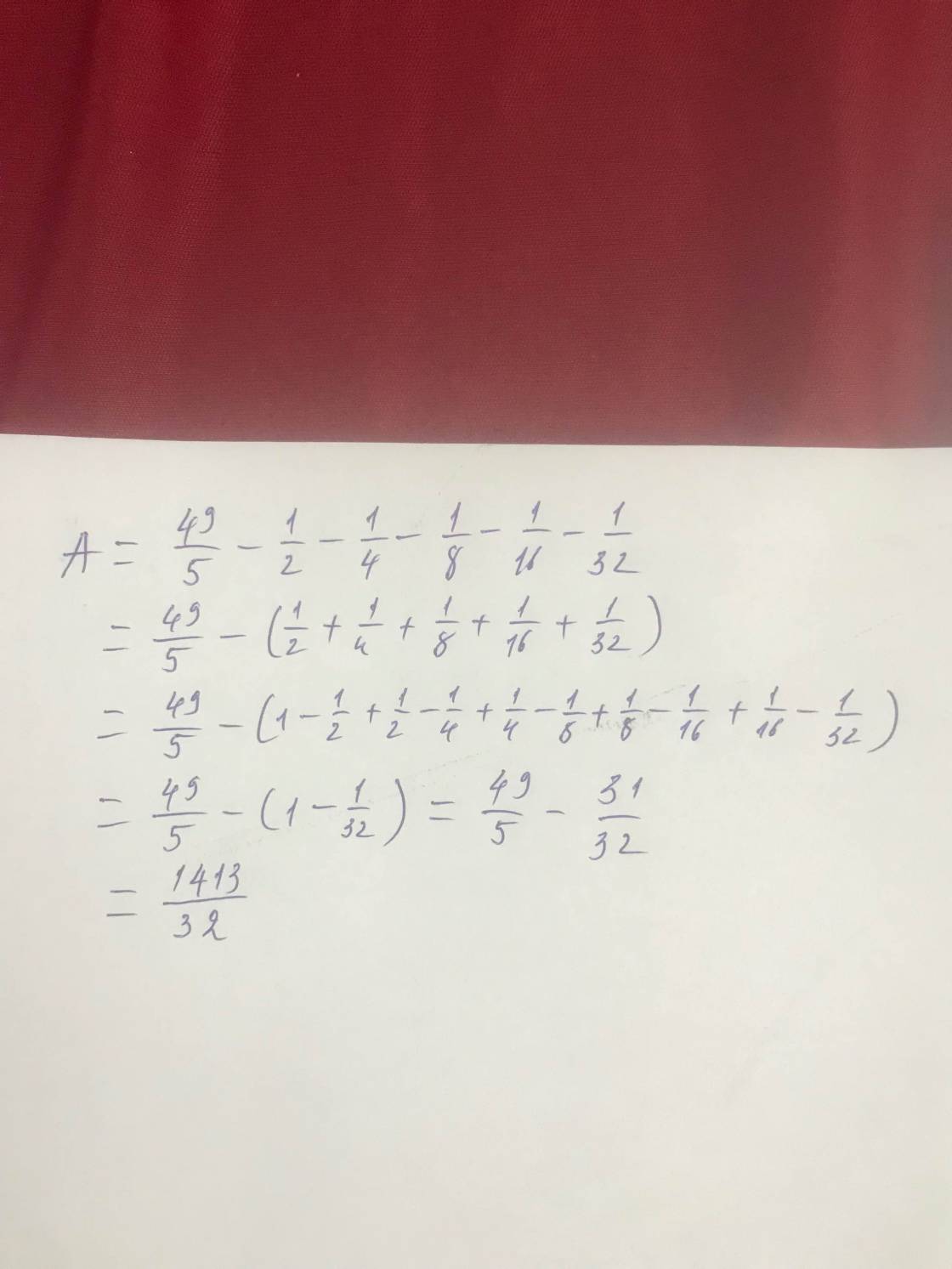
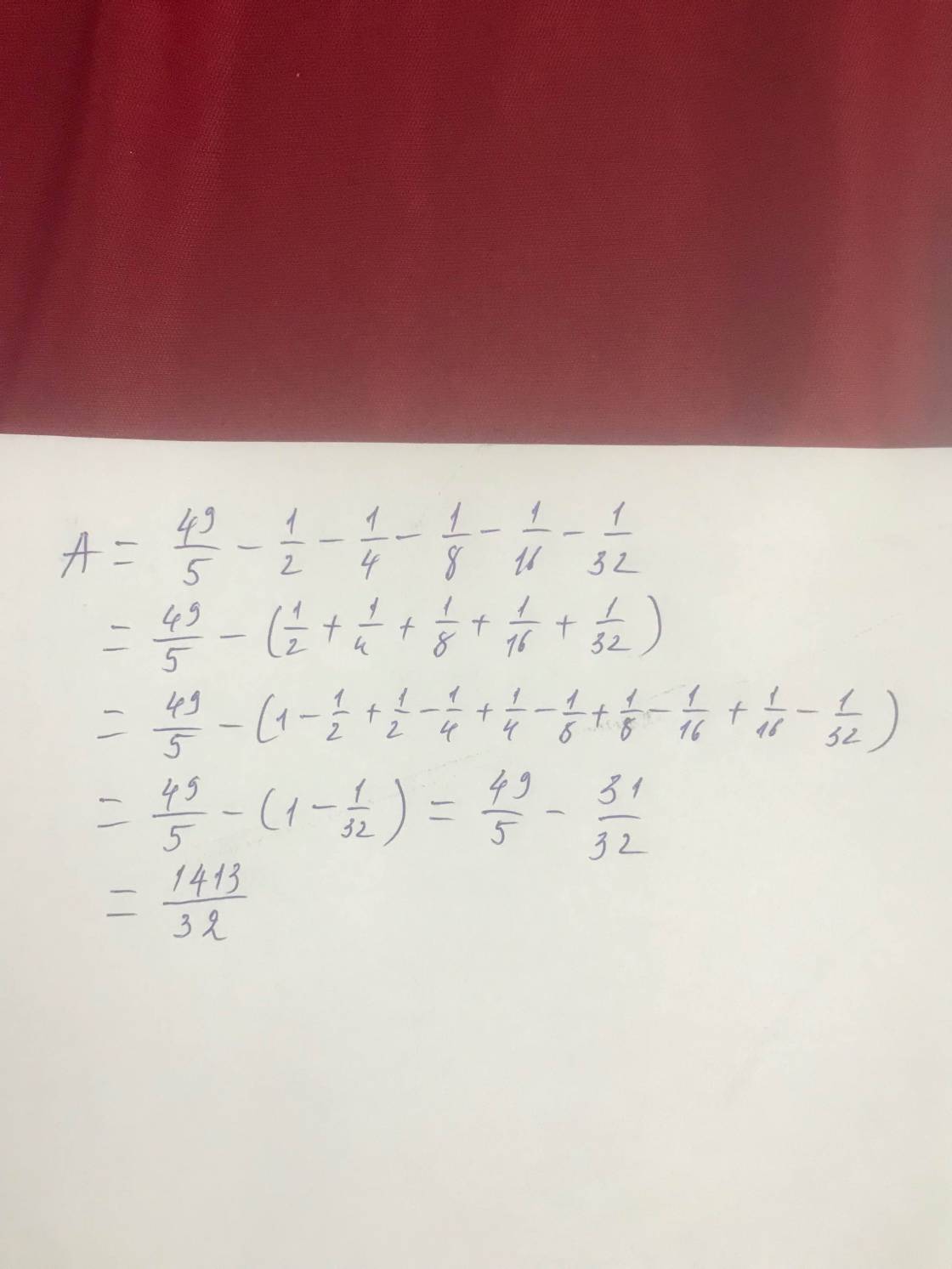
1/2+1/4+1/8+1/16+1/32+1/64
=(1/2+1/4+1/8)+(1/16+1/32+1/64)
=(4/8+2/8+1/8)+(4/64+2/64+1/64)
=7/8+7/64
=56/64+7/64
=63/64
B = \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\)
2 x B = 1 + \(\dfrac{1}{2}\)+ \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\)+ \(\dfrac{1}{32}\)
2 x B - B = 1 - \(\dfrac{1}{64}\)
B = \(\dfrac{63}{64}\)