Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
5 x − y + x + 2 y = 2 2 x + 3 y y + 1 2 . x − 1 2 = x y + 1 2
⇔ 2 x = 5 y x y + x − y − 1 2 = x y + 1 2 ⇔ 2 x = 5 y x y + x − y − 1 = x y + 1 x y + x − y − 1 = − x y − 1 ⇔ 2 x = 5 y x − y = 2 2 x y + x − y = 0
Ta có x − y = 2 .
Chọn đáp án B.
Chọn B.
+ Ta có các số 5x - y; 2x + 3y; x + 2y lập thành CSC nên suy ra
2( 2x + 3y) = 5x – y + x+ 2y hay 2x = 5y (1)
Các số (y + 1)2, xy + 1, (x – 1)2 lập thành CSN suy ra (xy + 1)2 = (y + 1)2(x – 1)2 ⇔ (4 + 2y – 2x)(4xy + 2x – 2y) = 0 (2)
Thay (1) vào (2) ta được: (4 + 2y – 5y)(10y2 + 5y – 2y) = 0
⇔ y(4 – 3y)(10y + 3) = 0 ⇔ y = 0, y = 4/3, y = -3/10.
Vậy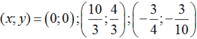 
Chọn A.
- Để: 1 + s i n x ; s i n 2 x ; 1 + s i n 3 x là ba số hạng liên tiếp của một cấp số cộng thì:
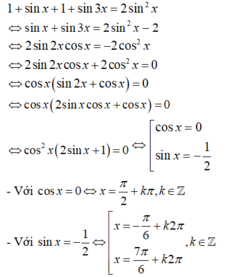
- Biểu diễn 3 họ nghiệm đó trên đường tròn lượng giác thì vị trí các điểm xuất hiện là: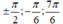 
. Do đó loại Đáp án B, C.
- Đáp án D. Thiếu nghiệm.
- Đáp án A. Đầy đủ nhất.
+) Với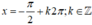 
thì vị trí điểm biểu diễn là: -π/2 ứng với k = 0
+) Với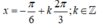 
thì vị trí điểm biểu diễn là: 
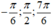ứng với k = 0,1,2.
Theo giả thiết ta có : \(\begin{cases}\left(5x-y\right)+\left(x+2y\right)=2\left(2x+3y\right)\\\left(y+1\right)^2\left(x-1\right)^2=\left(xy+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\xy+x+y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\y\left(5y\right)+5y+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{10}{3}\\y=\frac{4}{3}\end{cases}\) hoặc \(\begin{cases}x=0,y=0\\x=-\frac{3}{4},y=-\frac{3}{10}\end{cases}\)
Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
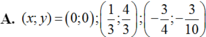
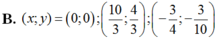
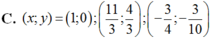
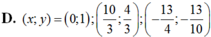
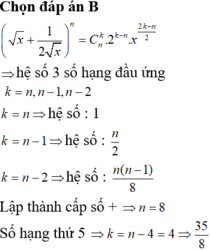
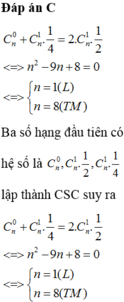
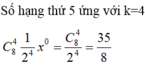
Do 3 số đầu là các số hạng liên tiếp của 1 CSC
\(\Rightarrow2\left(2x+3y\right)=5x-y+x+2y\)
\(\Leftrightarrow2x-5y=0\) \(\Rightarrow x=\frac{5y}{2}\)
Do các số sau là số hạng liên tiếp của 1 cấp số nhân
\(\Rightarrow\left(xy+1\right)^2=\left(y+1\right)^2\left(x-1\right)^2\)
\(\Rightarrow\left(\frac{5y^2}{2}+1\right)^2=\left(y+1\right)^2\left(\frac{5y}{2}-1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(y+1\right)\left(\frac{5y}{2}-1\right)=\frac{5y^2}{2}+1\\\left(y+1\right)\left(\frac{5y}{2}-1\right)=-\frac{5y^2}{2}-1\end{matrix}\right.\)
Bạn tự khai triển và giải 2 trường hợp này, chỉ là pt bậc 1 sau khi rút gọn